Általános megjegyzések a feladatokhoz
Először szerepel az adatok leírása, majd utána az adatokhoz kapcsolódó kérdések találhatóak. Próbáljatok meg a kérdéseket önállóan vagy csoportokban megoldani, de a megoldásokat csak az eredmények ellenőrzésére használjátok. Ha elakadtok, akkor is próbáljátok meg a megoldást a dokumentációkban (pl. a magyar nyelvű R segítség, Biostatisztika nem statisztikusoknak c. könyv, illetve az órán kiadott segédlet) megtalálni.
A feladatok megoldása általában mindig az alábbi "menetrend" szerint történik: Először mindig elemezzük az adatainkat grafikusan! Milyen eloszlásúak a változóink? Milyen típusúak a változóink (numerikus, faktor, stb.)? Készítsük el a kérdésnek megfelelő ábrát! Gondoljuk végig, hogy az 1. pont alapján használhatunk-e paraméteres tesztet? A gyakorlaton tanultak alapján válasszuk ki az alkalmazandó teszt típusát! Végezzük el a statisztikai elemzést!
Jó szórakozást!
1. Hallgatók biometrikus adatai
Egy korábbi kurzus során adatokat gyűjtöttünk a hallgatók testmagasságáról, súlyáról, szemszínéről, valamint fejszámolási gyorsaságáról. Az adatokat a kurzuson részt vevő hallgatók gyűjtötték. A magasságot cm-ben mérték két alkalommal (magassag1 és magassag2 nevű változók). A súly értékek kg-ban szerepelnek (bevallás alapján). A szemszín értelemszerűen az adott hallgató szeme színét jelöli, összesen három csoport alakult így ki. A számolási sebesség mérése úgy történt, hogy két kétjegyű számot kellett fejben összeadni, a számoláshoz eltelt időt mértük másodpercben. Az itt található kérdések egy részét már a gyakorlaton is elemeztük, most ismétlésképpen nézzük ezeket kiegészítve néhány másik kérdéssel, amit az órán nem néztünk!
Az adatok az alábbi helyen találhatóak: http://web.unideb.hu/~lendvai/teaching/hallgatok.csv
Az adatokat elemezve válaszolj az alábbi kérdésekre!
1.1. A csoport összes egyedét tekintve, mekkora a testsúly átlaga, szórása? Mi a medián súly értéke?
1.2. A testmagasságot kétszer mérték le a hallgatók. Ábrázold az első mérést a második függvényében! Értelmezd az ábrát!
1.3. Van-e különbség a két magasság mérés között?
1.4. Készíts egy új változót magasság néven, amiben kiszámolod a két mért magasság (tehát magasság1 és magasság2) átlagát!
1.5. Van-e szignifikáns különbség a fiúk és lányok testmagassága között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát! (Az elemzéshez és az ábrához használd az előző pontban létrehozott változót!)
1.6. Van-e szignifikáns különbség a fiúk és a lányok testsúlya között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
1.7. Az összes egyedet tekintve van-e szignifikáns kapcsolat a testsúly és a magasság között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát! (Az elemzéshez és az ábrához használd az 4. pontban létrehozott változót!)
1.8. Az összes egyedet tekintve van-e szignifikáns különbség a testsúlyban a különböző szemszínű egyedek között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
1.9. Eltér-e a szemszínek eloszlása az alábbi feltételezett eloszlástól: kék 10%, zöld 10%, barna 80%? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
1.10. Van-e összefüggés a számolási gyorsaság és a testsúly között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
1.11. Számoljunk egyfajta kondíció-indexet, ahol a testsúlyt elosztjuk a testmagassággal! Összefügg-e ez a változó a számolási gyorsasággal? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
2. Reggeli gabonapelyhek cukortartalma
Egy vizsgálatban megnézték, hogy mekkora egy áruház felső és alsó polcain található gabonapelyhek cukortartalma. (Az adatokat Sarah Sterling és Alex Greczek gyűjtötte 2004 decemberében a Meijer és Michigan-ben.)
Az adatok itt találhatóak: http://web.unideb.hu/~lendvai/teaching/cereals.csv
Az adatokat elemezve válaszolj az alábbi kérdésekre!
2.1. Van-e különbség a felső és alsó polcon található gabonapelyhek cukortartalmában?
segítség: Az adatokat célszerű úgy átalakítani, hogy a cukortartalom egy változó legyen, és a polc magasságát (felső vagy alsó) egy külön változó, pl. "polc" tartalmazza!
3. Olimpiai aranyérmes úszási eredmények
Az alábbi adattábla az olimpiai aranyérmes férfiak 1500m-es gyorsúszásának eredményeit tartalmazza 1896-tól 2004-ig. A z adattábla változói: name: az olimpiai bajnok neve time: az olimpiai bajnok úszási ideje (mp-ben) year: az olimpia éve nationality: az olimpiai bajnok nemzetisége (az ország 3 betűs rövidítése) kontinens: melyik kontinensről származik az olimpiai bajnok.
Az adatok itt találhatóak: http://web.unideb.hu/~lendvai/teaching/uszas.csv
Az adatokat elemezve válaszolj az alábbi kérdésekre!
3.1. Változott-e az egymást követő olimpiák során az úszási eredmény?
3.2. Hány olimpiai bajnok volt az egyes kontinensekről? Eltér-e ez az egyenletes eloszlástól (azaz, minden kontinens egyenlő arányban adott-e olimpiai bajnokot ebben a számban)?
3.3. Volt-e különbség az egyes kontinensek között az olimpiai bajnokok úszási idejében?
3.4. Mekkora volt az európai olimpai bajnokok közt a leggyorsabb, a leglassabb és a medián úszási eredmény?
A gyakorlati jegy megszerzéséért a 4. vagy az 5. feladatot kell megoldani, tetszés szerint lehet választani.
4. Hiperárak
Az adattábla a www.hiperarak.hu alapján készült. Különböző kategóriákban hasonlítja össze 4 országos áruházlánc áruházainak árait.
Az adatok itt találhatóak: http://web.unideb.hu/~lendvai/teaching/hiperarak.RData
Az adatokat elemezve válaszolj az alábbi kérdésekre!
4.1. Az összes termék közül melyik áruházban lehet a legolcsóbb és melyikben a legdrágább terméket kapni? (Tehát itt egyszerűen az a kérdés, hogy az adattáblában szereplő termékek közül melyik a legolcsóbb és a legdrágább, és ezeket melyik áruház(ak)ban lehet kapni).
4.2. Mekkora a Tesco-ban kapható chips típusú termékek átlagos ára és szórása?
4.3. Az összes terméket figyelembe véve van-e szignifikáns különbség az egyes áruházak árai között?
5. Alvás
Aki egy kicsit biológiaibb példát szeretne, annak itt egy másik, érdekes adatsor, ami különböző emlősök alvási idejét tartalmazza (egyebek mellett). A változók (ezeknek csak egy részét fogjuk elemezni, de nem szedtem ki a többit, hogy ha valakit érdekel, tudjon vele játszani):
species: az állat (angol) neve body_weight: az állat testsúlya (kg-ban) brain_weight: az állat agytömege (g-ban) slowwave: slow wave sleep, "nem álmodó alvás" (óra/nap) paradox: paradoxical sleep, azaz "álmodó alvás" (óra/nap) total: slowwave + paradox, azaz az összes alvás ideje (óra/nap) lifespan: maximum élethossz (években) gestation: terhesség (nap) predation: predációs index (1-5), ahol 1 a legkisebb esély, hogy ragadozónak esik áldozatul exposure: alvás kitettségi index (1-5), azaz mennyire veszélyeztetett az állat alvás közben, ahol 1 a legkevésbé veszélyeztetett (pl. egy védett üreg mélyén alvó állat) danger: összesített veszély index (1-5), ahol 1 a legkisebb veszély
Az adatok itt találhatóak: http://web.unideb.hu/~lendvai/teaching/sleep.csv
Az adatokat elemezve válaszolj az alábbi kérdésekre!
5.1. Melyik állat tölti a legtöbb és legkevesebb időt alvással egy nap? (A teljes alvással töltött időt nézzük!)
5.2. Összefügg-e szignifikáns mértékben a nem álmodó alvással töltött idő a predációs veszélyeztetettséggel?
5.3. Van-e szignifikáns összefüggés a 10 évnél rövidebb életű fajok álmodó és nem álmodó alvással töltött idejében?
Megoldások
1. Hallgatók biometrikus adatai
Az adatok beolvasása:
> hallgatók <- read.csv(file = "http://web.unideb.hu/~lendvai/teaching/hallgatok.csv", header = TRUE, sep = ";")
1.1. A csoport összes egyedét tekintve, mekkora a testsúly átlaga, szórása? Mi a medián súly értéke?
Először nézzük meg az adatokat grafikusan! Ha pl. van valami elírás az adatokban (valaki pl. 75 kg helyett 750 kg), akkor az azonnal kiderül.
> plot(hallgatók$súly)
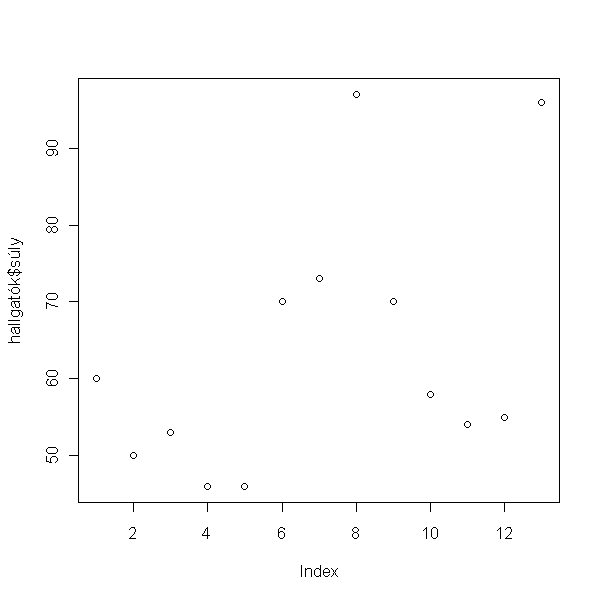
Nézzük a kérdésre adott választ numerikusan:
> mean(hallgatók$súly)
[1] 63.69231
> sd(hallgatók$súly)
[1] 16.98717
> median(hallgatók$súly)
[1] 58
1.2. A testmagasságot kétszer mérték le a hallgatók. Ábrázold az első mérést a második függvényében! Értelmezd az ábrát!
> plot(magasság1 ~ magasság2, data = hallgatók, ylab = "testmagasság (cm) első mérés", xlab = "testmagasság (cm) második mérés")
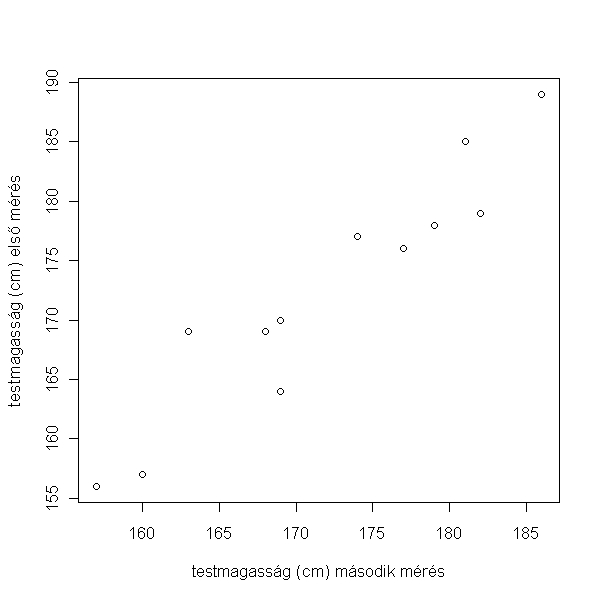
Az összefüggés nyilván szoros, az eltérést a mérési hiba okozza.
1.3. Van-e különbség a két magasság mérés között?
Ehhez nem árt az adatokat átalakítani.
> mag <- c(hallgatók$magasság1, hallgatók$magasság2)
> mérés <- c(rep(1, length(hallgatók$magasság1)), rep(2, length(hallgatók$magasság2)))
> t.test(mag ~ mérés, paired = TRUE, var.equal = TRUE)
Paired t-test
data: mag by mérés
t = -0.0804, df = 12, p-value = 0.9373
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.162416 2.008570
sample estimates:
mean of the differences
-0.07692308
A paired = TRUE specifikáció azért kell, mert itt páros mérésekről van szó, azaz a két minta nem független, hisz ugyanazokat az embereket mértük le kétszer.
A két minta között messze nincs különbség (p = 0.937).
1.4. Készíts egy új változót magassag néven, amiben kiszámolod a két mért magasság (tehát magasság1 és magasság2) átlagát!
> hallgatók$magasság <- (hallgatók$magasság1 + hallgatók$magasság2)/2
1.5. Van-e szignifikáns különbség a fiúk és lányok testmagassága között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát! (Az elemzéshez és az ábrához használd az előző pontban létrehozott változót!)
> plot(magasság ~ nem, data = hallgatók, main = "Ivari dimorfizmus a testmagasságban", xlab = "Nem", ylab = "Testmagasság (cm)")
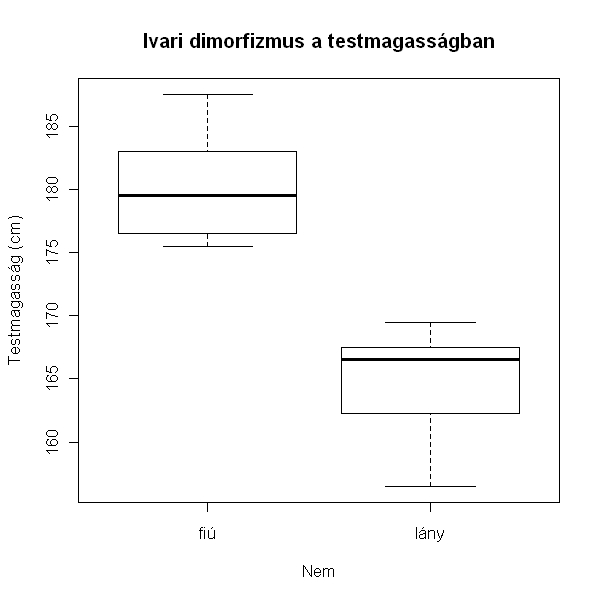
Ábrázolhatjuk ezeket az adatokat oszlopdiagrammon is. Ehhez először kiszámoljuk az átlag magasságot nemenként:
> mag.fiúk <- mean(hallgatók$magasság[hallgatók$nem == "fiú"])
> mag.lányok <- mean(hallgatók$magasság[hallgatók$nem == "lány"])
Majd ezeket összefűzzük, és elnevezzük az értékeket:
> mag.fiúlány <- c(mag.fiúk, mag.lányok)
> names(mag.fiúlány) <- c("fiú", "lány")
Ugyanezt megtehetjük egyszerűbben is a tapply paranccsal. A két megközelítés ugyanazt az eredményt adja:
> mag.fl <- tapply(hallgatók$magasság, hallgatók$nem, mean)
> mag.fl
fiú lány
180.2500 164.5714
> mag.fiúlány
fiú lány
180.2500 164.5714
Kiszámoljuk az adatok standard hibáját (standard error, SE):
> mag.SE <- tapply(hallgatók$magasság, hallgatók$nem, sd)/sqrt(length(hallgatók$magasság))
Jöhet az oszlopdiagram:
> library(gplots)
> barplot2(mag.fl, plot.ci = TRUE, ci.u = mag.fl + mag.SE, ci.l = mag.fl, xlab = "Nem", ylab = "Testmagasság (cm)", ylim = c(0,
+ 200))
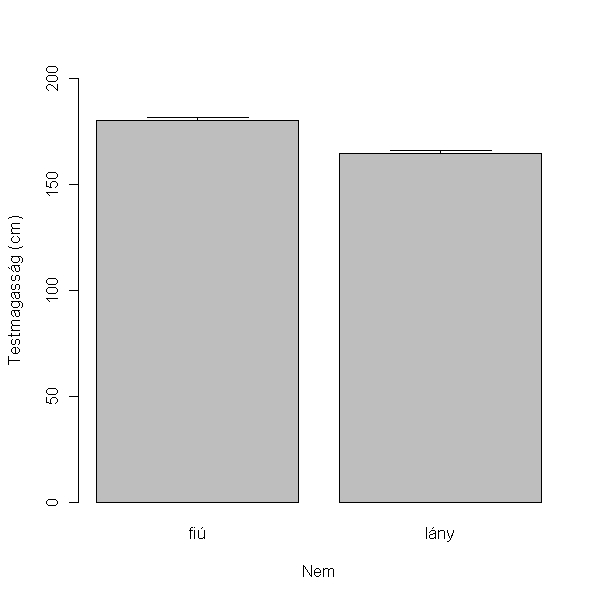
Nézzük meg, hogy milyen a magasság adatok eloszlása!
> hist(hallgatók$magasság, ylab = "Gyakoriság", xlab = "Testmagasság (cm)")
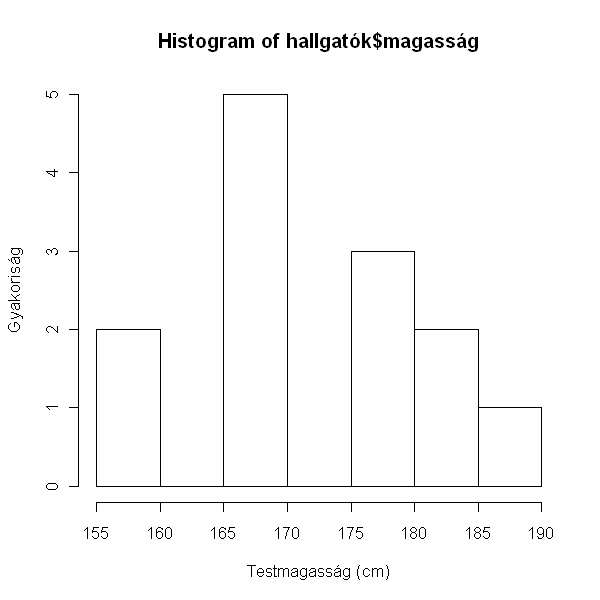
Az eloszlás normálnak tűnik, persze a kevés adat miatt kicsit "foghíjas". Tehát használhatunk paraméteres tesztet.
Két csoport különbségét t-próbával elemezhetjük:
> t.test(magasság ~ nem, data = hallgatók, var.equal = TRUE)
Two Sample t-test
data: magasság by nem
t = 5.8985, df = 11, p-value = 0.0001033
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
9.82822 21.52892
sample estimates:
mean in group fiú mean in group lány
180.2500 164.5714
Gyakorlásképp írjuk le a nullhipotézist és az alternatív hipotézist:
H0: A fiúk és a lányok testmagassága nem különbözik. HA: A fiúk és a lányok testmagassága különbözik.
A p érték jóval kisebb, mint 0.05, ezért a nullhipotézist elvetjük. Az eredményeket így prezentálhatjuk:
"A vizsgált mintában a fiúk és a lányok testmagassága szignifikánsan különbözött (t = 5.898, df = 11, p < 0.001)."
1.6. Van-e szignifikáns különbség a fiúk és a lányok testsúlya között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
Ez ugyanez, mint fent, csak a súlyra Tehát: ábrát készítünk, megnézzük az adatok eloszlását, és ha lehet, t-próbával elemezzük az adatokat (mivel két független csoportot hasonlítunk össze).
> plot(súly ~ nem, data = hallgatók, xlab = "Nem", yab = "Súly (kg)")
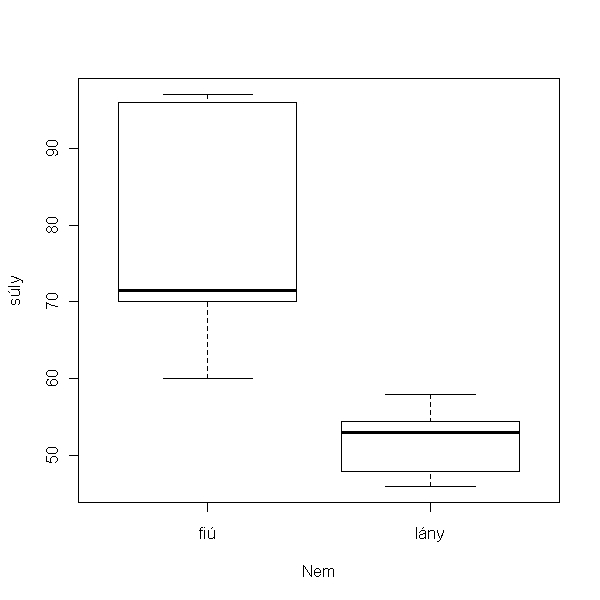
> hist(hallgatók$súly)
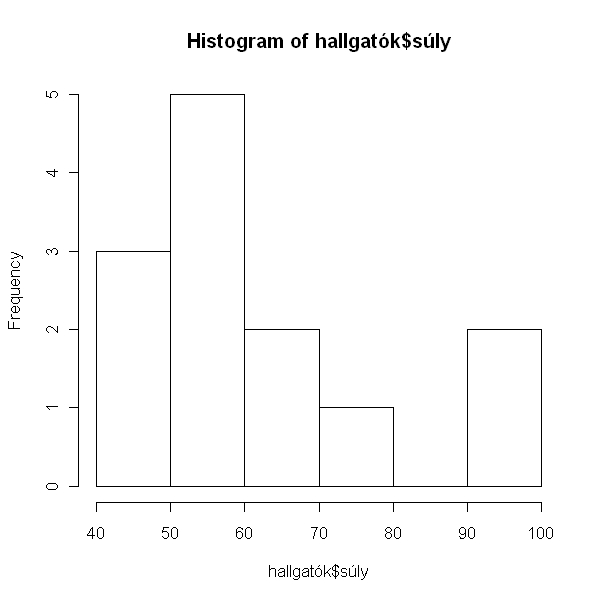
Az eloszlás nagyobb mintában valószínűleg normál lenne, itt sem vészes az eltérés. Csinálhatjuk a t-próbát (gyakorlásképp), de azért megnézzük a nem-paraméteres párját is, a Mann-Whitney U-tesztet, hogy hogy kell csinálni.
> t.test(súly ~ nem, data = hallgatók)
Welch Two Sample t-test
data: súly by nem
t = 4.019, df = 5.773, p-value = 0.007544
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
9.999665 41.905097
sample estimates:
mean in group fiú mean in group lány
77.66667 51.71429
U-test:
> wilcox.test(súly ~ nem, data = hallgatók, paired = FALSE)
Wilcoxon rank sum test with continuity correction
data: súly by nem
W = 42, p-value = 0.003318
alternative hypothesis: true location shift is not equal to 0
1.7. Az összes egyedet tekintve van-e szignifikáns kapcsolat a testsúly és a magasság között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát! (Az elemzéshez és az ábrához használd az 4. pontban létrehozott változót!)
Mivel itt két folytonos változó kapcsolatára vagyunk kíváncsiak, scatterplot-ot készítünk és korreláció analízist végzünk:
> plot(súly ~ magasság, data = hallgatók, xlab = "Magasság (cm)", ylab = "Súly (kg)")
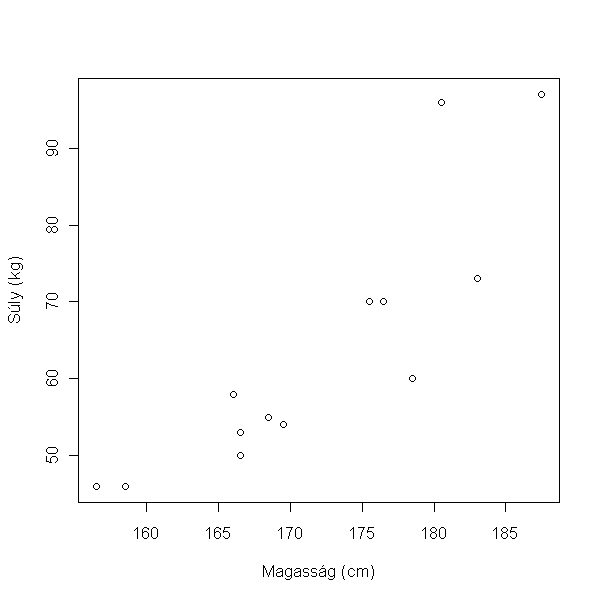
Azt, hogy a kapcsolat szignifikáns-e elemezhetjük korreláció analízissel:
> cor.test(hallgatók$magasság, hallgatók$súly)
Pearson's product-moment correlation
data: hallgatók$magasság and hallgatók$súly
t = 5.8603, df = 11, p-value = 0.0001092
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6134770 0.9606346
sample estimates:
cor
0.8702897
vagy lineáris modellel (lineáris regresszió):
> lin.mod1 <- lm(súly ~ magasság, data = hallgatók)
> summary(lin.mod1)
Call:
lm(formula = súly ~ magasság, data = hallgatók)
Residuals:
Min 1Q Median 3Q Max
-14.293 -5.285 -1.125 3.507 18.539
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -208.4551 46.5025 -4.483 0.000927 ***
magasság 1.5840 0.2703 5.860 0.000109 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8.739 on 11 degrees of freedom
Multiple R-squared: 0.7574, Adjusted R-squared: 0.7354
F-statistic: 34.34 on 1 and 11 DF, p-value: 0.0001092
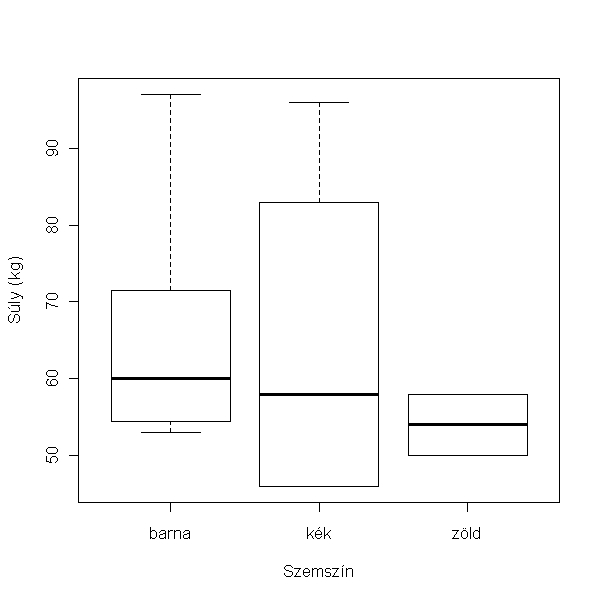
1.8. Az összes egyedet tekintve van-e szignifikáns különbség a testsúlyban a különböző szemszínű egyedek között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
Itt azt kérdezzük, hogy több csoport átlaga között van-e szignifikáns eltérést, varianciaanalízist (ANOVA) végzünk. Az adatelemzést itt is az adatok ábrázolásával kezdjük:
> plot(súly ~ szem, data = hallgatók, xlab = "Szemszín", ylab = "Súly (kg)")
Az egyes csoportok változatossága között nagy a különbség, ez itt amiatt van, hogy az adatsor nagyon pici, de ezzel most nem foglalkozunk. Az elemzés hasonlóan történne egy nagyobb adattáblán is. Gyakorlásként ajánlom az alábbi, lényegesen nagyobb adatsort, amin számos hasonló elemzést el lehet végezni, ráadásul a mi adatsorunkhoz képest egy csomó érdekes változót tartalmaz: http://tinyurl.com/3ytcdbo
Visszatérve a mi kis adatsorunkhoz, először nézzük meg, hogy a szemszín változó faktorként van-e kódolva
> is.factor(hallgatók$szem)
[1] TRUE
Akkor jöhet a lineáris modell (ANOVA), az elemzés szintaxisa így néz ki:
> lin.mod2 <- lm(súly ~ szem, data = hallgatók)
> anova(lin.mod2)
Analysis of Variance Table
Response: súly
Df Sum Sq Mean Sq F value Pr(>F)
szem 2 227.8 113.88 0.352 0.7116
Residuals 10 3235.0 323.50
A különböző szemszínű hallgatók súlya nem különbözik egymástól szignifikáns mértékben (F2,10 = 0.352, p = 0.711).
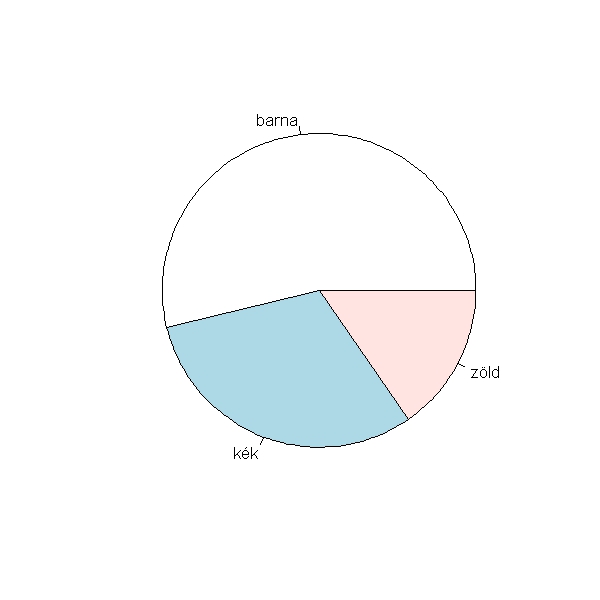
1.9. Eltér-e a szemszínek eloszlása az alábbi feltételezett eloszlástól: kék 10%, zöld 10%, barna 80%? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
Nézzük először az adatok grafikus ábrázolását! Ez lehetséges kördiagrammal (általában nem javasolt ábratípus):
> pie(table(hallgatók$szem)/length(hallgatók$szem))
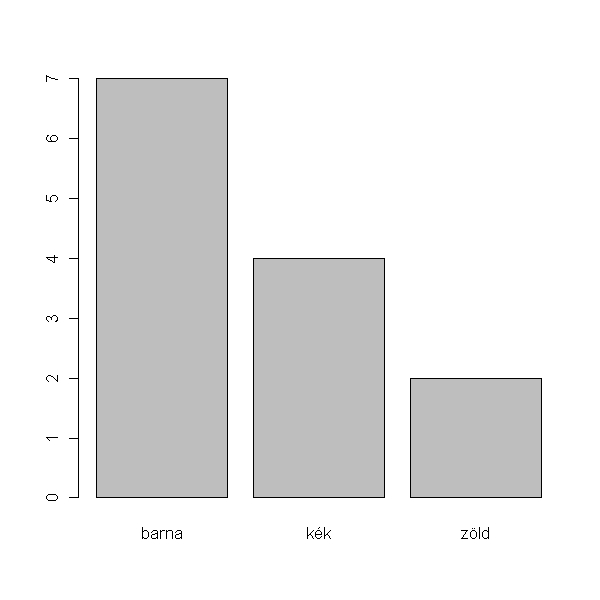
Talán jobb, ha oszlopdiagrammot készítünk:
> barplot(table(hallgatók$szem))
Mégjobb, ha a konkrét gyakoriságok helyett az arányokat ábrázoljuk és mellette feltűntetjük a várt értékeket
> tapasztalt <- table(hallgatók$szem)/length(hallgatók$szem)
> várt <- c(0.8, 0.1, 0.1)
> barplot(rbind(tapasztalt * 100, várt * 100), beside = T, ylim = c(0, 100), names.arg = c("barna", "kék", "zöld"), legend.text = c("tapasztalt",
+ "várt"), axis.lty = 1, ylab = "Szemszínek aránya (%)")
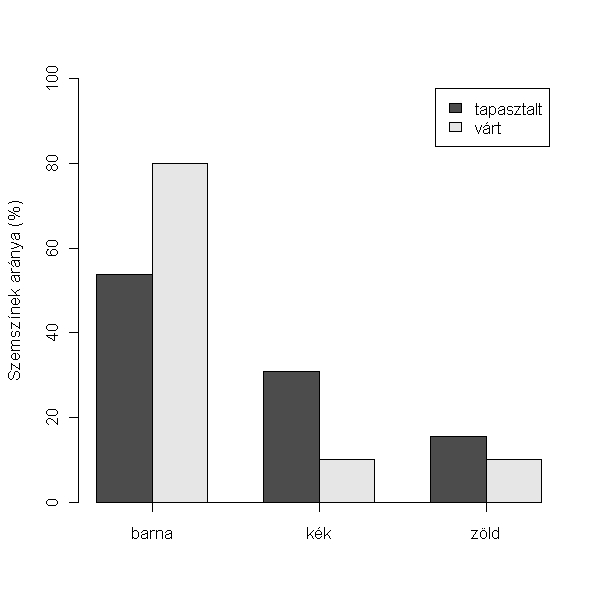
Először tehát létrehoztunk egy vektort tapasztalt névvel, ami kiszámítja, hogy mekkora az egyes szemszínek aránya. (A table funkció kiszámolja, hogy hány egyed van szemszínenként, majd ezt elosztottuk a teljes mintahosszal, amit a length fügvénnyel határoztunk meg.) Majd a feladatban megadott értékeknek megfelelően létrehoztunk egy várt nevű vektort.) A barplot függvény már ismerős, az új elem a legend.text amivel az oszlopok magyarázatát adjuk meg, az axis.lty = 1 pedig csak annyit csinál, hogy húz egy x tengelyt, de ez már csak "csicsa". :-)
Egy várt (elméleti) és egy tapasztalt eloszlás közötti különbséget Chi-négyzet teszttel elemezhetjük. A szintaxis a következő:
> chisq.test(x = table(hallgatók$szem), p = várt)
Chi-squared test for given probabilities
data: table(hallgatók$szem)
X-squared = 7.0962, df = 2, p-value = 0.02878
Itt egy figyelmeztető üzenetet kapunk, ami megint csak az alacsony mintaszám miatt van. Ha a tapasztalt gyakoriságok valamelyike kisebb, mint 5, ezt az üzenetet kapjuk. De ezt kiküszöbölhetjük a sim = TRUE szintaxissal, ami a p értéket egy szimulációs eljárással becsüli, ez a konkrét esetben megbízhatóbb:
> chisq.test(x = table(hallgatók$szem), p = várt, sim = TRUE)
Chi-squared test for given probabilities with simulated p-value (based on 2000 replicates)
data: table(hallgatók$szem)
X-squared = 7.0962, df = NA, p-value = 0.04048
Az eredmény szerint a szemszínek tapasztalt eloszlása eltér a 80-10-10%-tól.
1.10. Van-e összefüggés a számolási gyorsaság és a testsúly között? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
> plot(számolás ~ súly, data = hallgatók, xlab = "Súly (kg)", ylab = "Fejszámolási gyorsaság (mp)")
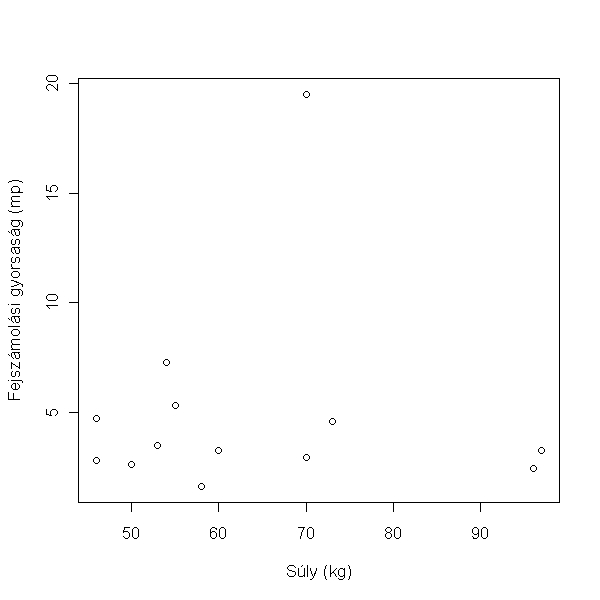
Van egy kilógó adatpontunk, ami befolyásolhatja az eredményt (bár az ábra alapján valószínűleg nem fogja). Mindenesetre biztosabb nem paraméteres korreláció analízist végezni, amit a method = "spearman" kiegészítéssel tudunk megtenni.
> cor.test(hallgatók$súly, hallgatók$számolás, method = "spearman")
Spearman's rank correlation rho
data: hallgatók$súly and hallgatók$számolás
S = 382.0497, p-value = 0.8722
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.04958697
A fejszámolás sebessége és a testsúly között nincs összefüggés (r = -0.049, p = 0.872).
1.11. Számoljunk egyfajta kondíció-indexet, ahol a testsúlyt elosztjuk a testmagassággal! Összefügg-e ez a változó a számolási gyorsasággal? Ábrázold az eredményeket és közöld a hozzá tartozó statisztikát!
Kondíció index számolása:
> hallgatók$kondi <- hallgatók$súly/hallgatók$magasság
> plot(számolás ~ kondi, data = hallgatók, xlab = "Kondíció index", ylab = "Fejszámolási gyorsaság (mp)")
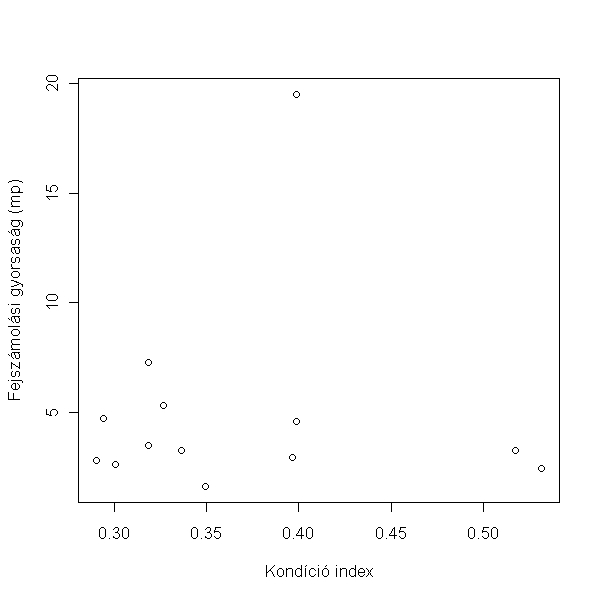
Ugyanaz érvényes, mint az előző feladatnál:
> cor.test(hallgatók$kondi, hallgatók$számolás, method = "spearman")
Spearman's rank correlation rho
data: hallgatók$kondi and hallgatók$számolás
S = 388, p-value = 0.8348
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.06593407
Szintén nincs összefüggés.
2. Reggeli gabonapelyhek cukortartalma
2.1. Van-e különbség a felső és alsó polcon található gabonapelyhek cukortartalmában?
Az adatok beolvasása:
> pehely <- read.csv(file = "http://web.unideb.hu/~lendvai/teaching/cereals.csv", header = TRUE, sep = ";")
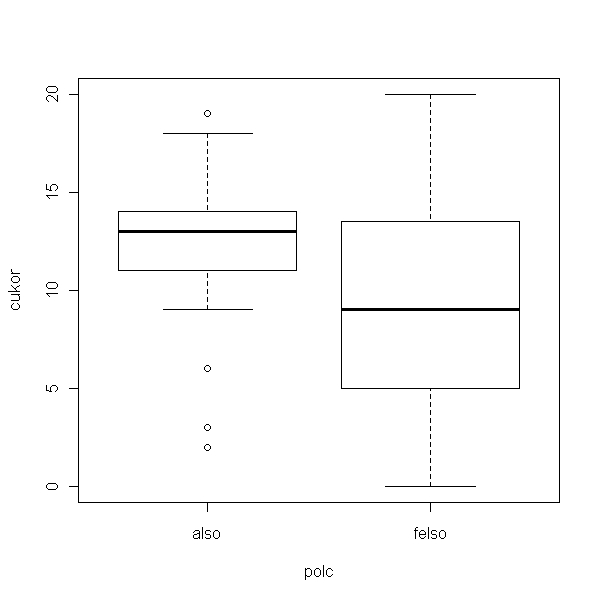
Ahogy azt a feladatban jeleztem, érdemes az adatokat átalakítani.
> cukor <- c(pehely$felso, pehely$also)
> polc <- c(rep("felso", length(pehely$felso)), rep("also", length(pehely$also)))
> polc <- factor(polc)
> plot(cukor ~ polc)
Nézzük az adatok eloszlását:
> hist(cukor)
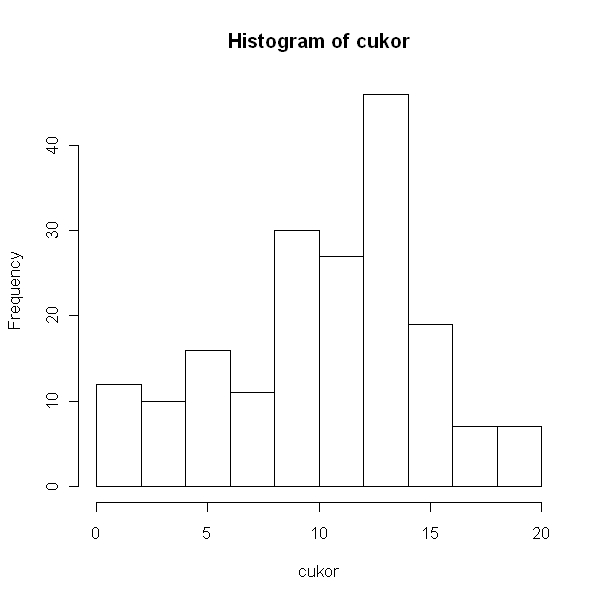
Úgy tűnik, hogy a két csoportban eltér az adatok varianciája, biztosabb így a var.equal = T opciót kihagyni.
> t.test(cukor ~ polc)
Welch Two Sample t-test
data: cukor by polc
t = 5.5579, df = 164.601, p-value = 1.08e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
2.223412 4.673664
sample estimates:
mean in group also mean in group felso
12.522222 9.073684
A különbség magasan szignifikáns: tehát az áruházakban az alacsonyabb cukortartalmú gabonapelyheket helyezik a felső polcokra. El lehet rajta gondolkozni, vajon miért.
3. Olimpiai aranyérmes úszási eredmények
Az adatok beolvasása:
> uszas <- read.csv(file = "http://web.unideb.hu/~lendvai/teaching/uszas.csv", sep = ";", header = TRUE)
3.1. Változott-e az egymást követő olimpiák során az úszási eredmény?
(Most csinálunk egy változót felirat névvel, hogy ezt ne kelljen később újra beírni, ha egy másik ábrát készítünk. Vegyük észre, hogy így az ábra ylab részében nem idézőjel közé tesszük a szöveget, hanem az objektumunkra hivatkozunk!)
> felirat <- "Aranyérmes ideje (mp)"
> plot(time ~ year, data = uszas, xlab = "Olimpia éve", ylab = felirat)
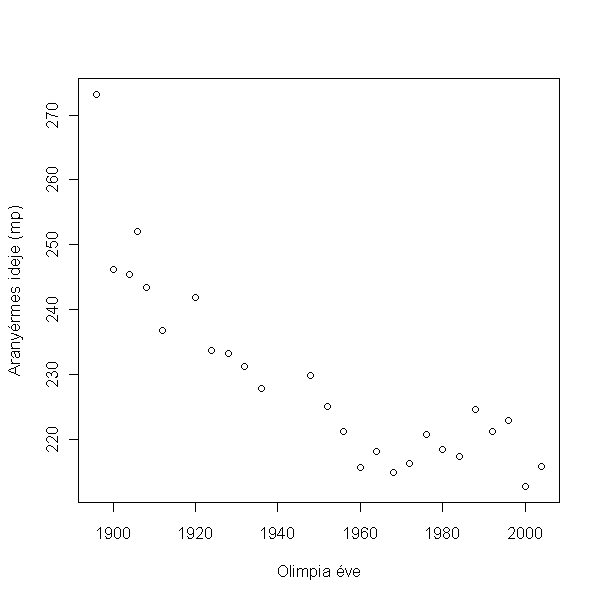
Úgy tűnik, van összefüggés. Lássunk rá egy statisztikai elemzést. Mivel itt két folytonos változónk van, ezért ezt megint csak korreláció elemzéssel vagy lineáris regresszióval végezhetjük.
Nézzük előbb az adatok eloszlását, vajon normál eloszlásúak-e?
> hist(uszas$time, xlab = felirat)
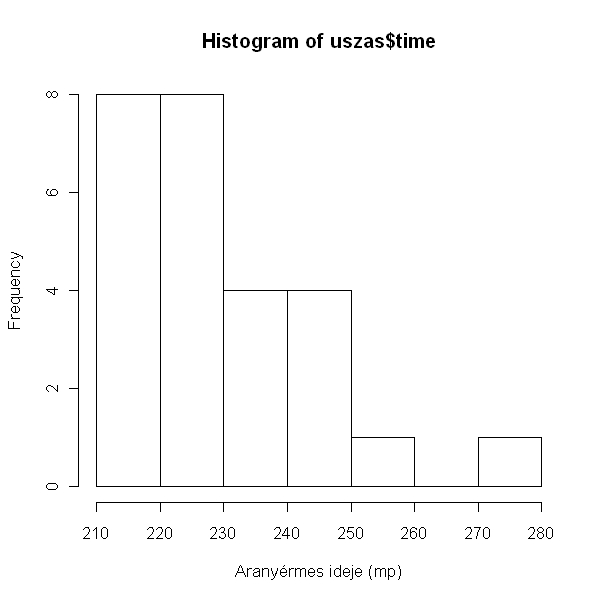
A változó eloszlása balra eltolt, nem normál, valamint a legelső adat eléggé kilóg a többi közül, ezért talán itt is biztonságosabb a Spearman-féle nem paraméteres korrelációt végezni:
> cor.test(uszas$year, uszas$time, method = "spearman")
Spearman's rank correlation rho
data: uszas$year and uszas$time
S = 5457.433, p-value = 1.118e-08
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.865789
Az elemzés erős negatív összefüggést mutat ami magasan szignifikáns (r = -0.865, p < 0.001). Tehát idővel az úszási eredmények egyre jobbak lettek.
(Meg kell jegyezni, hogy az összefüggés látszólag nem lineáris, és pontosan erre is számítanánk, így itt a korreláció elemzés nem a legjobb módszer. Ráadásul az adatpontok nem is feltétlenül függetlenek, ezért itt finomabb statisztikai modellekkel is lehetne ezt elemezni, ami figyelembe veszi a nem-linearitást és az adatok nem függetlenségét, de ez már a "haladó" kurzus része lenne. :-) Elégedjünk most meg annyival, hogy a nullhipotézist, miszerint nincs összefüggés az évek és az úszási eredmények között, elvethetjük. A korrelációs modellünk szerint az úszási eredmények idővel csökkennek. )
3.2. Hány olimpiai bajnok volt az egyes kontinensekről? Eltér-e ez az egyenletes eloszlástól (azaz, minden kontinens egyenlő arányban adott-e olimpiai bajnokot ebben a számban)?
Ez könnyű:
> table(uszas$kontinens)
Afrika Amerika Ausztrália Európa
5 4 4 13
Az elemzést Chi-négyzet teszttel végezhetjük:
> chisq.test(x = table(uszas$kontinens))
Chi-squared test for given probabilities
data: table(uszas$kontinens)
X-squared = 8.7692, df = 3, p-value = 0.03252
(Mivel az egyenletes eloszlástól való eltérést teszteljük a várt eloszlást nem is kell megadni, a program automatikusan ehhez képest számolja a tesztet).
Úgy tűnik tehát, hogy az olimpiai bajnokok a véletlentől eltérő arányban jönnek az egyes kontinensekről, Európa pl. láthatóan több bajnokot adott.
3.3. Volt-e különbség az egyes kontinensek között az olimpiai bajnokok úszási idejében?
Lássunk rá egy ábrát!
> plot(time ~ kontinens, data = uszas, xlab = "kontinens", ylab = felirat)
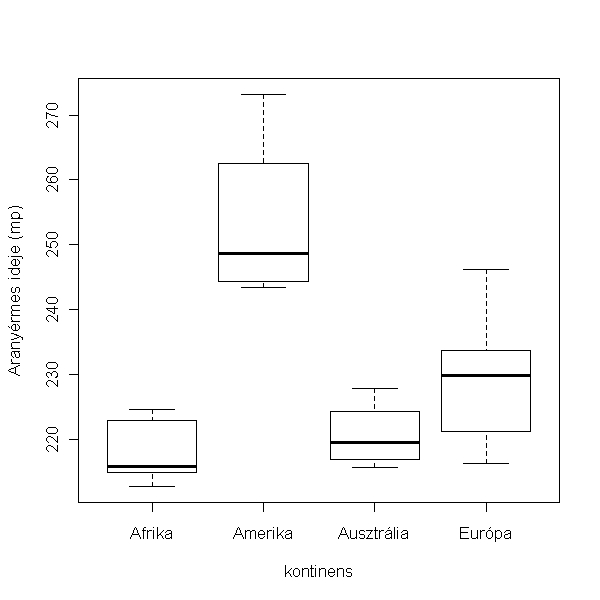
Az látszik, hogy az amerikaiak a leglassabbak, és az európaiak is a lassabbak egy kicsit, mint az afrikaiak és az ausztrálok. Vajon szignifikáns ez a különbség? Ezt variancia analízissel teszteljük.
> uszas.model1 <- lm(time ~ kontinens, data = uszas)
> summary(uszas.model1)
Call:
lm(formula = time ~ kontinens, data = uszas)
Residuals:
Min 1Q Median 3Q Max
-12.323 -6.932 -1.930 4.893 19.700
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 218.160 4.113 53.047 < 2e-16 ***
kontinensAmerika 35.340 6.169 5.729 9.2e-06 ***
kontinensAusztrália 2.390 6.169 0.387 0.7022
kontinensEurópa 10.463 4.839 2.162 0.0418 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.196 on 22 degrees of freedom
Multiple R-squared: 0.6377, Adjusted R-squared: 0.5883
F-statistic: 12.91 on 3 and 22 DF, p-value: 4.459e-05
> anova(uszas.model1)
Analysis of Variance Table
Response: time
Df Sum Sq Mean Sq F value Pr(>F)
kontinens 3 3275.0 1091.66 12.909 4.459e-05 ***
Residuals 22 1860.4 84.57
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Ez az összefüggés szignifikáns, tehát van statisztikai különbség az egyes kontinensek aranyérmeseinek idejében. A summary tábla azt mutatja, hogy Afrikához képest a többi kontinens eredménye eltér-e (csak azért veszi a függvény Afrikát referenciának, mert ábácé sorrendben ez van legelől, de szükség esetén ezt át lehet állítani). Az látszik, hogy Amerika és Európa úszói is lassabbak az Afrikaiaknál. Az anova parancs pedig a faktor összes szintjét figyelembe véve egyetlen p értéket ad, hogy a kontinensek különböznek-e. Ez is alátámasztja azt, hogy igen. Mielőtt azonban elkeserednénk (vagy épp fellelkesednénk), fel kell tennünk a kérdést, hogy vajon nem lehet-e a dolog mögött az, hogy az európai aranyérmesek régebben nyertek, amikor még az úszási idők hosszabbak voltak, az afrikaiak meg mostanában, amikor már jobb eredményeket úsznak? Nézzük meg!
Ehhez jelöljük a különböző kontinensekről származó versenyzőket külön jellel. Ezt a plot függvényben a pch argumentum módosításával tudjuk megtenni. De akár színezhetjük is a col argumentum módosításával. Utána a legend fügvénnyel egy jelmagyarázatot adunk.
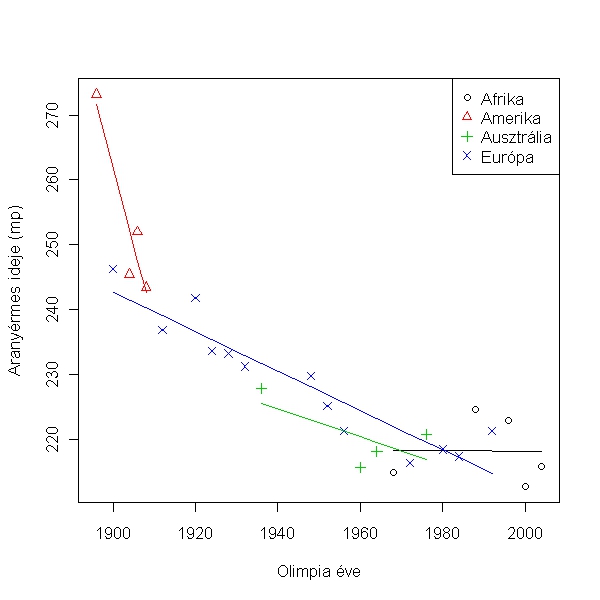
> kont <- as.numeric(uszas$kontinens)
> plot(time ~ year, data = uszas, xlab = "Olimpia éve", ylab = felirat, pch = kont, col = kont)
> legend("topright", legend = levels(uszas$kontinens), pch = 1:4, col = 1:4)
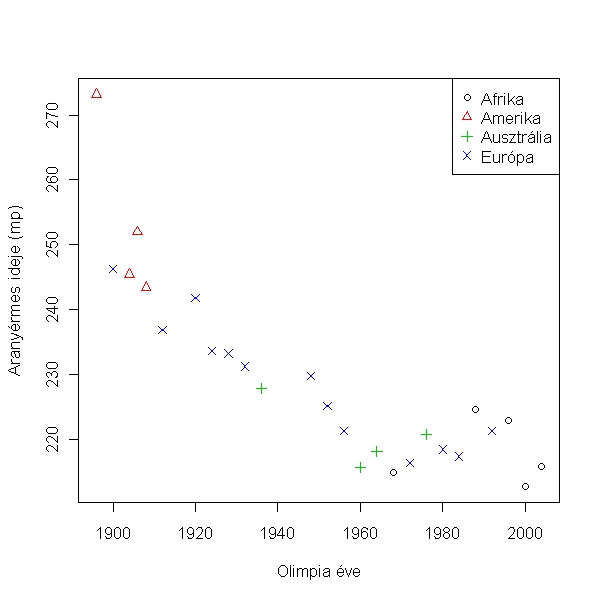
Jól látszik, hogy az amerikaiak csak a XIX. század végén és a XX. század elején nyertek ebben a számban olimpiát! Tehát ez magyarázhatja a kontinensek közötti különbséget. Ennek vizsgálatához kontrollálnunk kell arra, hogy melyik évben tartották az olimpiát (amiről már az előbb kiderítettük, hogy számít az úszási eredményben):
> uszas.model2 <- lm(time ~ year * kontinens, data = uszas)
> summary(uszas.model2)
Call:
lm(formula = time ~ year * kontinens, data = uszas)
Residuals:
Min 1Q Median 3Q Max
-6.8892 -2.3124 -0.4357 3.2270 6.5264
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.205e+02 3.141e+02 0.702 0.491687
year -1.181e-03 1.578e-01 -0.007 0.994109
kontinensAmerika 4.643e+03 9.909e+02 4.686 0.000184 ***
kontinensAusztrália 4.211e+02 4.367e+02 0.964 0.347660
kontinensEurópa 6.003e+02 3.256e+02 1.844 0.081748 .
year:kontinensAmerika -2.421e+00 5.183e-01 -4.670 0.000190 ***
year:kontinensAusztrália -2.137e-01 2.210e-01 -0.967 0.346346
year:kontinensEurópa -3.031e-01 1.638e-01 -1.851 0.080685 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.498 on 18 degrees of freedom
Multiple R-squared: 0.9291, Adjusted R-squared: 0.9015
F-statistic: 33.69 on 7 and 18 DF, p-value: 4.36e-09
> anova(uszas.model2)
Analysis of Variance Table
Response: time
Df Sum Sq Mean Sq F value Pr(>F)
year 1 3796.5 3796.5 187.6697 5.821e-11 ***
kontinens 3 523.1 174.4 8.6187 0.0009245 ***
year:kontinens 3 451.8 150.6 7.4443 0.0019133 **
Residuals 18 364.1 20.2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Az eredmények azt mutatják, hogy a kontinens és az év hatása szignifikáns interakcióban van egymással. Ez azt jelenti, hogy bár az általános trend az, hogy a későbbi olimpiákon gyorsabbak az úszók (year: F1, 18 = 187.669, p < 0.001), és különbség van a kontinensek között (F3, 18 = 8.619, p < 0.001), az egyes kontinenseken az évek hatása más és más (year:kontinens interakció, F3, 18 = 7.444, p = 0.002) (kerekítve). Tehát az illesztett egyenes meredeksége más és más a különböző kontinensen: míg az amerikaiak a modern olimpiák elején nyertek ebben a számban, ott az idők gyorsan javultak, így az összefüggés erősen negatív, az afrikai úszók az utóbbi évtizedekben törtek fel, de náluk már nem látható az évekkel a javulás. Az alábbi ábra szemlélteti ezt:
|
Warning
|
Végezetül: bár ez az elemzés már többet mond, mint már korábban említettem, ez az elemzés még mindig nem teljesen korrekt, mert a lineáris variancia analízis számos fontos feltétele sérül, de erre most a bevezető kurzusban nem tértünk ki. Bonyolultabb statisztikai eljárásokkal ezeket az elemzéseket lehet tovább finomítani, de nekünk most ennyi bőven elég. |
3.4. Mekkora volt az európai olimpai bajnokok közt a leggyorsabb, a leglassabb és a medián úszási eredmény?
Ez így a végére megint könnyű.
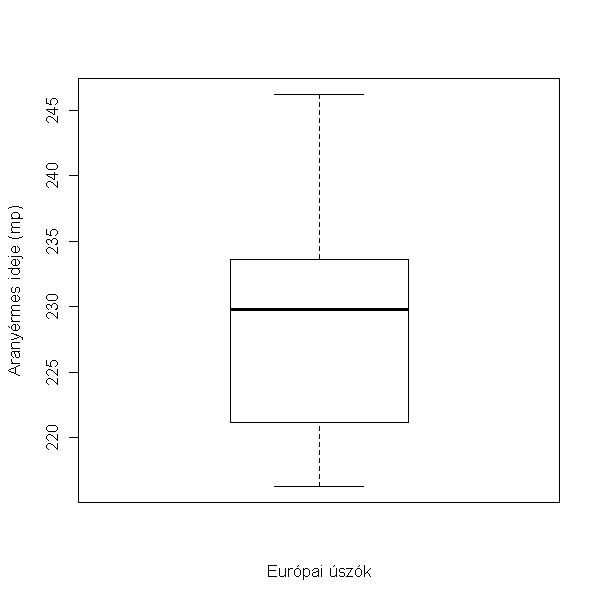
> boxplot(uszas$time[uszas$kontinens == "Európa"], xlab = "Európai úszók", ylab = felirat)
Szám szerint a leggyorsabb:
> max(uszas$time[uszas$kontinens == "Európa"])
[1] 246.2
Leglassabb:
> min(uszas$time[uszas$kontinens == "Európa"])
[1] 216.3
Medián:
> median(uszas$time[uszas$kontinens == "Európa"])
[1] 229.8
4. Hiperárak
Ezt a megoldást nyilván nem mutatom meg :-)
Viszont, akit esetleg érdekel, itt látható, hogy hogy készítettem az adatokat.
A cél, a hiperarak.hu oldalon feltűntetett adatok alapján meghatározni, hogy van-e szignifikáns különbség az ott szerepeltetett négy áruház árai között.
Mivel az adatok nem érhetők el valamilyen "adatbázis barát" táblázat formában, az adatokat ki kellett másolni az egyes lapokról. Mivel az összes árat túl munkaigényes lett volna bemásolni, így első lépésben véletlen mintát vettünk az oldal által felsorolt kategóriákból. Az oldalon 7 kategória volt található, ezeken belül további alkategóriák. Először tehát létrehoztam egy listát, ami tartalmazza azt, hogy az egyes kategóriákban hány alkategória szerepel:
> kategoriak <- list(1, 1:6, 1:9, 1:8, 1:16, 1:8, 1:2)
Majd mindegyikből véletlenszerűen kiválasztunk egyet, aminek az árait elemezni fogjuk.
beállítjuk a véletlenszám generátort, hogy mindenki ugyanazt az eredményt kapja:
> set.seed(1)
majd kisorsoljuk a vizsgálandó alkategóriákat:
> unlist(lapply(kategoriak, function(x) sample(x, 1)))
[1] 1 3 6 8 4 8 2
A sós kategóriában a "készétel" alkategória lett kisorsolva, de az oldalon ehhez az alkategóriához csak két ár tartozik, így ez nem alkalmas az elemzésre, választunk egy másik kategóriát, hátha itt több szerencsével (nagyobb mintaszámmal) járunk:
> set.seed(2)
> sample(kategoriak[[3]], 1)
[1] 2
Az így készült adatokat Excelbe másoltam, eltávolítottam a szóközöket, a "Ft"-okat és a "*"-okat meg a "-"-eket. Az adatfile-t beolvassuk az R-be:
> arak1 <- read.csv("http://web.unideb.hu/~lendvai/teaching/Hiperarak.csv", header = T, sep = ";")
Első körben ki kell szedni azokat az adatokat, ahol nincs minden áruházhoz adat:
> arak2 <- arak1[!is.na(arak1$Auchan) & !is.na(arak1$Tesco) & !is.na(arak1$Interspar) & !is.na(arak1$Cora), ]
Utána átalakítjuk a file-t, hogy az elemzéseknek megfelelő formátumban legyen:
> ár <- c(arak2$Auchan, arak2$Tesco, arak2$Interspar, arak2$Cora)
> hossz <- dim(arak2)[1]
> bolt <- c(rep("Auchan", hossz), rep("Tesco", hossz), rep("Interspar", hossz), rep("Cora", hossz))
> termék <- rep(arak2$alkategoria, 4)
> árak <- data.frame(ár, bolt, termék)
> save(árak, file = "hiperarak.Rdata")
Jó munkát!