GÁSPÁR
VILMOS
A megszelídített káosz
A káoszszabályozás
A káoszszabályozás címszót hiába keressük a Magyar értelmező kéziszótár 1972-es kiadásában. Az általánosan elterjedt vélekedés - egészen a legutóbbi időkig - ugyanis az volt, hogy ami kaotikus (nem megjósolható), az ab ovo nem kontrollálható. Például a Wolf-díjas Freeman Dyson 1988-ban megjelent könyvének "Engineers Dreams" című fejezetében [1] a következő, eléggé egyértelmű állásfoglalás olvasható: "Egy kaotikus folyamat általában nem jósolható meg és nem is szabályozható. Nem jósolható meg, mert már egy kis zavaró hatás is a folyamat exponenciálisan növekvő perturbációját eredményezi. Nem szabályozható, mert a kicsiny zavarások csak más kaotikus állapothoz, nem pedig valamilyen stabil, megjósolható alternatívához vezetnek. Von Neumann tévedett, amikor úgy képzelte, hogy a megfelelő helyeken alkalmazott kicsiny taszigálásokkal minden instabil mozgás stabillá bökdöshető." Az elmúlt évtized kutatásainak eredményeként azonban Neumann János álma végül mégiscsak beteljesülni látszik: a káosz megszelídíthető. Ennek módszereit ismertetem különböző kaotikus kémiai rendszerekkel végzett kísérleteink eredményeit felhasználva [2-7].
Kaotikusan viselkedő rendszerek szabályozására elsőként Hübler és Lüscher javasolt megoldást [8]. Módszerük, amely a differenciálegyenlet-rendszer szisztematikus átalakításán alapul, igen jól működik modellszámításokban, de nehezen alkalmazható valós rendszerekre. Az első, kísérletileg megvalósíthatónak tűnő módszert Ott, Grebogi és Yorke (OGY) közölte 1990-ben [9]. Cikkük robbanásszerű fejlődést idézett elő a témakör kutatásában. Egy évtizeddel később a Physics Reports összefoglaló cikkében Boccaletti és szerzőtársai már közel kétszáz közleményre hivatkozva ismertették a káoszszabályozással kapcsolatos kutatások legjelentősebb elméleti és kísérleti eredményeit [10]. Az OGY-módszert sikerrel alkalmazták egyszerű mechanikai gépek, komplex hidrodinamikai rendszerek, elektronikus eszközök, lézerek, sejtrendszerek (szív- és agyszövetminták) és közgazdasági modellek kaotikus viselkedésének szabályozására. Az általunk vizsgált kaotikus kémiai és elektrokémiai rendszerek szabályozására mi az OGY-algoritmus egyszerűsített változatát alkalmaztuk [11]. E módszer részleteinek ismertetése előtt azonban definiálni szeretném, hogy pontosan mit is értünk a káosz szabályozásán, s mi is történik valójában a káosz megszelídítésekor.
A káoszszabályozás azt jelenti, hogy a véletlenszerűnek tetsző kaotikus (aperiodikus) "mozgást" egy (vagy több) paraméter kicsiny változtatásával (perturbáció) előre jelezhető (periodikus) "mozgássá" alakítjuk.Nem tekintjük káoszszabályozásnak azt, ha a paraméter új értéke a kaotikus tartományon kívülre esik, mert ez nem más, mint a káosz megszüntetése egyszer s mindenkorra. Ezzel szemben, a káosz szabályozásakor a rendszer dinamikai állapotát megszabó paraméterértékek mindvégig a kaotikus tartományban maradnak. Ezt igen könnyen ellenőrizhetjük, ugyanis a perturbációt megszüntetve a rendszer (egy rövid átmeneti szakaszt követően) ismét kaotikusan fog viselkedni.
A káoszszabályozás kiindulópontja az, hogy egy kaotikus rendszer mozgása nem akármilyen rendezetlen módon, hanem - bizonyítottan - mindig az ún. kaotikus attraktoron történik.1 A szabályozás módszereit két nagy csoportba osztjuk. A szakaszos módszerek alkalmazásakor a szabályozó paraméter értékét csak jól meghatározott időközönként, a folytonos módszerekben pedig folyamatosan változtatjuk. A perturbációk nagyságát mindkét esetben a rendszer állapotának ismeretében határozzuk meg.
A kaotikus attraktor rekonstrukciója
Egy szakaszos módszer (például az OGY-algoritmus) alkalmazásához ismernünk kell a) a dinamikai változók fázisterében kialakuló kaotikus attraktort és b) az attraktor változását a paraméterek változtatásának hatására. A kísérleti munka során azonban legtöbbször nincs lehetőségünk arra, hogy egy dinamikai rendszer összes változóját nyomon követhessük. Nagyon gyakran csak egyetlen változó (például egy köztitermék koncentrációja) vagy több változó értékétől függő összetett "jel" (például elektródpotenciál, fényelnyelés, az áramkör teljes árama stb.) mérésére van lehetőségünk. Ha csak egyetlen jel időbeli változását, x(t), ismerjük, akkor az attraktort az ún. rekonstrukciós eljárással [14] állítjuk elő a következő módon. Egy m-dimenziós térben ábrázoljuk az x(t), x(t-t), x(t-2t), ..., x[t-(m-1)t] értékeket, ahol m a rekonstruált fázistér dimenziója, tpedig az eljárás során alkalmazott ún. késleltetési idő. Ennek értéke elvileg tetszőlegesen választható. Gyakorlati tapasztalat, hogy t optimális értéke a kaotikus oszcillációt jellemző átlagos "periódusidő" egytizede és egyharmada között van. Ugyancsak kísérleti tapasztalat, hogy a káosz szabályozásához nem mindig szükséges az eredeti attraktorral topológiailag ekvivalens m-dimenziós attraktort előállítani. Kisszámú (2-3) dinamikai változóval leírható, ún. alacsony dimenziójú dinamikai rendszerekben (a legtöbb ismert kaotikus kémiai rendszer ilyen) ugyanis elegendő az x(t) és x(t-t) értékeket használni. Ezzel a módszerrel állítottuk elő például egy rézelektród felületének elektrokémiai (anódos) tisztítása során mérhető kaotikus áramoszcilláció alacsony dimenziójú kaotikus attraktorát (1. ábra).
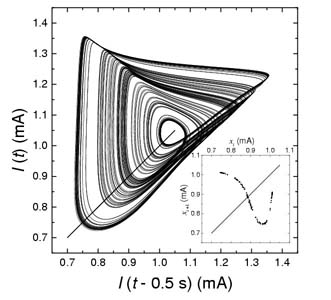
1. ábra.
Rézelektród foszforsavban lejátszódó anódos oldódása során mért
áramoszcilláció kaotikus attraktora. A belső ábrán látható egydimenziós
leképezést az attraktor és a diagonális egymást követő metszéseihez
rendelhető xi+1 és xi értékekből szerkesztettük meg
[3]
A kaotikus leképezés és a káosz szabályozása
A káosz szabályozásához ismernünk kell a rendszer mozgását a kaotikus attraktoron. Ezért a fázistérben elhelyezünk egy hipersíkot (Poincaré-síkot)2 úgy, hogy az elmetssze az attraktort. Ezután nyomon követjük a kaotikus mozgást, és rögzítjük az azonos, előre kiválasztott irányból érkező pályavonalak és a Poincaré-sík ismétlődő metszéséhez tartozó x1, x2, ..., xi, ..., xn metszéspontok koordinátáit. Mivel a kaotikus rendszer determinisztikus és autonóm [12], az xivektor értéke egyértelműen meghatározza a következő metszéshez tartozó xi+1 vektor értéket. Más szóval, a kaotikus rendszer dinamikáját egyértelműen leírhatjuk egy egyszerű diszkrét leképezéssel:
![]() .
(1)
.
(1)
Ezek a diszkrét leképezések ugyanolyan tulajdonságokkal rendelkezhetnek, mint a Játsszunk káoszt! című cikkben [15] bemutatott "pókhálódiagramok", csak itt nem két, hanem több térbeli dimenzióban kell elképzelnünk az iterációt. A leképezés x- "stacionárius pontját", ahol
![]() ,
(2)
,
(2)
a leképezés fixpontjának nevezzük. Mivel a fixpontban xi+1=xi, az instabil pont egészen biztosan része annak az egyperiódusú zárt pályának (P_1), amely az egyszerű oszcillációhoz rendelhető. Ha a leképezést csak a minden második metszésre vonatkozó adatokból készítjük el, akkor ez az instabil fixpont a kétperiódusú periodikus pályához (P_2) rendelhető stb. A kaotikus áramoszcillációt mutató réz-ortofoszforsav elektrokémiai rendszerben az áramadatokból rekonstruált attraktor kétdimenziós, s így a Poincaré-sík helyett elegendő egy egyenest definiálni. A metszéspontokból szerkesztett (xi+1 vs. xi) és (xi+2 vs. xi) egydimenziós leképezések az 1. és 2. ábrán láthatók. A pontok (mindkét ábrán) egy-egy jól meghatározott görbére esnek. Talán ezek létezése demonstrálja legszebben (bár mint tudjuk, a szépség nem tudományos kategória) a káosz determinisztikus eredetét és a káoszban uralkodó rendet.
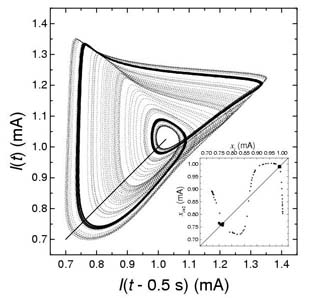
2. ábra.
Stabilizált kétperiódusú (P_2) áramoszcilláció zárt pályavonala a réz
elektrokémiai oldódásához rendelhető kaotikus attraktor belsejében. A
belső ábrán látható egydimenziós leképezést a kaotikus attraktor és a
diagonális minden második metszéshez rendelhető xi+2, illetve
xi értékekből szerkesztettük meg [3]
Egy szabályos
oszcilláció "fenntartásához" - más szóval egy tetszőleges periodikus
pályához tartozó instabil fixpont stabilizálásához - a kaotikus rendszert
először is a kívánt fixpont közelébe kell terelnünk. A másik lehetőség az,
hogy türelmesen megvárjuk azt a pillanatot, amikor a rendszer a fixpont
közelébe kerül. Mivel a kaotikus rendszer ergodikus, ez előbb-utóbb be is
következik [13]. Az ezt követő káoszszabályozás pedig lényegében nem más,
mint egy (vagy több) paraméter alkalmas megváltoztatása annak érdekében,
hogy a pályavonal és a Poincaré-sík következő metszése a fixpont kis
közelségében (ideális esetben pontosan a fixpontban) történjen meg. Az
1. és 2. ábrán látható kaotikus áramoszcilláció
szabályozására mi az egyszerűsített OGY-algoritmust alkalmaztuk [11]. A
továbbiakban ezt az eljárást fogom ismertetni, és a szakirodalomban
elterjedt angol elnevezés: Simple Proportinal
Feedback3 kezdőbetűiből képzett rövidítést (SPF)
fogom használni.
| Az
SPF-algoritmus szerinti káoszszabályozás lépései (csak egydimenziós
leképezéssel leírható kaotikus rendszerek esetén
alkalmazható):
1. a
kaotikus attraktor rekonstrukciója; |
A káoszszabályozás egyszerű szakaszos módszere
Az SPF-módszer alapja az a kísérleti megfigyelés, hogy az alacsony dimenziójú kaotikus rendszerekben a szabályozó paraméterek értékének kicsiny megváltoztatásakor képződő új kaotikus attraktor nagyon hasonló az eredetihez. Ennek megfelelően az új attraktorból szerkeszthető új leképezés is nagyon hasonló lesz az eredetihez. Feltételezzük, hogy a paraméter perturbálásának hatására az egydimenziós leképezés egyszerűen csak párhuzamosan eltolódik az alkalmazott koordináta-rendszer átlója mentén (3. ábra). Egyszerű geometriai megfontolások alapján a paraméterperturbáció értékének kiszámítására alkalmas ún. "szabályozási formula" a következőképpen vezethető le.
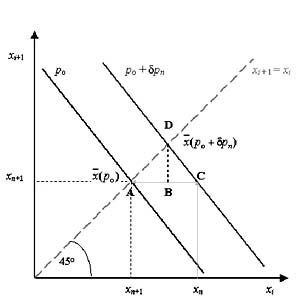
3. ábra. Az SPF-módszer szerinti káoszszabályozás geometriai értelmezése
Legyen p
a vizsgált kaotikus rendszer egyik paramétere, amelyet a szabályozás során
változtatunk. Tegyük fel, hogy pşpo értéknél a
rendszer kaotikus. Az egydimenziós leképezés ![]() fixpontjának
értékét (a pókhálódiagramok esetén alkalmazott eljáráshoz hasonlóan) a
leképezés és a diagonális metszéspontjából határozzuk meg (lásd 1.
és 2. ábra). A fixpont instabil, ha a leképezés fixpontbeli
meredeksége abszolút értékben egynél nagyobb.
fixpontjának
értékét (a pókhálódiagramok esetén alkalmazott eljáráshoz hasonlóan) a
leképezés és a diagonális metszéspontjából határozzuk meg (lásd 1.
és 2. ábra). A fixpont instabil, ha a leképezés fixpontbeli
meredeksége abszolút értékben egynél nagyobb.
Legyen a
leképezés értéke az n-edik metszéskor xn. Célunk
az, hogy a következő, (n+1)-edik metszés pontosan a fixpontban
történjen, azaz xn+1 =![]() teljesüljön.
Ezt úgy próbáljuk meg elérni, hogy a paraméter értékét az "iterációs"
ciklus alatt pontosan annyival (dpn) változtatjuk meg,
hogy az így előállított új leképezés pontosan az eredeti leképezés
instabil fixpontjába juttassa a rendszert. Ehhez először ismernünk kell
xn távolságát (dxn) a fixponttól, mely
az ábráról leolvasva:
teljesüljön.
Ezt úgy próbáljuk meg elérni, hogy a paraméter értékét az "iterációs"
ciklus alatt pontosan annyival (dpn) változtatjuk meg,
hogy az így előállított új leképezés pontosan az eredeti leképezés
instabil fixpontjába juttassa a rendszert. Ehhez először ismernünk kell
xn távolságát (dxn) a fixponttól, mely
az ábráról leolvasva:
![]() .
(3)
.
(3)
A paraméter
megváltoztatásával (a leképezés párhuzamos eltolásával) a fixpont is
eltolódik. Az eltolódás nagysága (![]() ) az ábra
szerint:
) az ábra
szerint:
![]() .
(4)
.
(4)
Tételezzük fel, hogy a fixpont eltolódása egyenesen arányos a paraméterperturbációval:
![]() ,
(5)
,
(5)
ahol K az arányossági tényező. A (4) és (5) egyenletek alapján:
![]() .
(6)
.
(6)
Feltételeztük, hogy a leképezések párhuzamosak. Meredekségük (m) a 3. ábra szerint
![]() (7)
(7)
melyből
a ![]() szakasz hossza:
szakasz hossza:
![]() (8)
(8)
A (3), (6) és (8) egyenletek alapján:
![]() (9)
(9)
ahol g =(m -1)K/m. A (9) egyenletből egyszerű átrendezéssel megkapjuk az SPF-módszer szerinti szabályozási formulát:
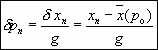 (10)
(10)
A (10) egyenlet szerint tehát a káosz szabályozásához szükséges visszacsatolás (a perturbáció nagysága) egyenesen arányos az n-edik metszéspont fixponttól vett távolságával az egydimenziós leképezésen. Innen származik a módszer elnevezése. A g szabályozási állandó értékét a (9) egyenlet szerint számítjuk ki més K értékének kísérleti meghatározása után.
Mivel az adatgyűjtés pontossága a kísérleti technika által mindig korlátozott, a rendszer kaotikus jellegéből - a kezdeti feltételekre való érzékenységből - az következik, hogy a perturbáció hatására a rendszer - nagy valószínűséggel - nem pontosan a kívánt fixpontba, hanem csak annak közelébe kerül. Ha újabb perturbációt nem alkalmazunk, a pályavonalak előbb-utóbb eltávolodnak az instabil fixpont környezetéből, és a rendszer továbbra is kaotikusan fog viselkedni. A káosz sikeres szabályozásához tehát az szükséges, hogy a 8., 9. és 10. lépéseket ciklikusan végrehajtsuk. Az ismételt perturbációk hatására a pályavonalak egyre közelebb kerülnek a fixponthoz, s így a perturbációk is egyre kisebbek lesznek. Ha a rendszer végül pontosan a fixpontba kerül, akkor további perturbációra már nincs szükség - a paraméter értéke azonos az eredetivel, ám most az aperiodikus viselkedés helyett előre jelezhető periodikus oszcillációt figyelhetünk meg. A káoszt megszelídítettük!
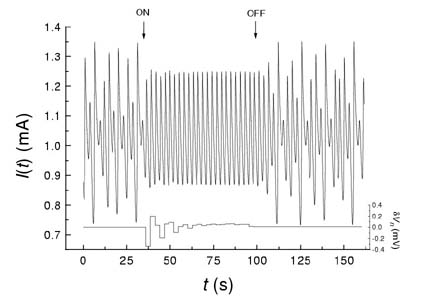
4. ábra.
Kaotikus áramoszcilláció szabályozása a réz-ortofoszforsav elektrokémiai
rendszerben [3]
A 4. ábrán rézelektród ortofoszforsavban lejátszódó anódos oldódása során mért kaotikus áramoszcilláció szabályozását követhetjük nyomon. Az SPF-algoritmus szerint először meghatároztuk a (10) egyenletben szereplő állandók értékeit, majd elkezdtük alkalmazni a szakaszos paraméterperturbációt (ON). Az áram- idő görbe igazolja, hogy sikerrel stabilizáltuk a P_1 típusú oszcillációt. Az alsó görbén látható, hogy a káoszszabályozás során alkalmazott dVn (mV) potenciálperturbáció egyre csökkenő mértékű volt, vagyis az egydimenziós leképezésen egyre közelebb kerültünk a P_1 oszcillációnak megfelelő instabil fixponthoz. A várakozásnak megfelelően az algoritmus kikapcsolása után (OFF) az áram ismét kaotikusan oszcillált, azaz a káoszt nem megszüntettük, hanem valóban szabályoztuk [3].
A szakaszos módszerek előnye az, hogy a fixpont körüli dinamika ismeretében pontos képletet tudunk adni a perturbáció nagyságának kiszámítására. Kiss István Zalánnal olyan módszert fejlesztettünk ki, amely akkor is sikeresen alkalmazható, ha a (10) egyenletnek megfelelő képletet nem tudjuk kísérletileg meghatározni [4]. Módszerünkben ún. mesterséges neuronhálózatokat "tanítunk" meg kaotikus rendszerek dinamikájának elemzésére, s ezt a "tudást" hasznosítjuk a káoszszabályozás automatizálására.
Az SPF-algoritmus csak azokban a szerencsés esetekben alkalmazható sikeresen, amikor a kaotikus dinamika jól jellemezhető egydimenziós leképezéssel, és az attraktor alakváltozása is könnyen megjósolható. A bonyolultabb rendszerekre kínál megoldást az OGY-elmélet [9], s pontosan ez tette a módszert széles körben ismertté.
A káoszszabályozás folytonos módszerei
Ha az instabil fixpont ún. Ljapunov-kitevője (a ponttól való eltávolodás sebességét jellemző mértékszám) olyan nagy (˝l˝>>1), hogy két egymást követő metszés koordinátáira nem tudunk megbízható jóslást tenni, akkor a szakaszos módszerek már nehezen használhatók. Erre az esetre Hübinger és munkatársai dolgoztak ki egy eljárást, amelyben nem egy, hanem több Poincaré-síkot alkalmaznak, s így egy ciklus alatt több perturbációval stabilizálják a rendszert [16]. Végtelen számú síkot feltételezve eljutunk a folytonos módszerekhez. Ezek teljes elméletét még nem dolgozták ki.
Az ún. folytonosan késleltetett visszacsatolás alkalmazásakor a folytonosan változó perturbáció nagyságát, dp(t),a következő képlettel számítjuk ki:
![]() ,
(11)
,
(11)
ahol x(t) a rendszer egy mért dinamikai változójának t időpontbeli értéke, t az ún. késleltetési idő, C pedig a szabályozási állandó. Könnyen belátható, hogy ez az eljárás, amelyet a szakirodalomban Pyragas-módszernek neveznek [17], a kísérletező szempontjából sokkal egyszerűbb. A módszer további előnye, hogy a perturbációk folytonos alkalmazása miatt a kísérleti zaj okozta hiba kisebb. Hátránya viszont az, hogy nem tudjuk előre megtervezni, melyik periodikus pályát is fogjuk szabályozni. Ráadásul a szabályozási állandót és a késleltetési időt is - általában - próbálgatással kell megállapítani.
A Pyragas-módszert alkalmazva tudtuk például csatolt kaotikus elektrokémiai oszcillátorok szinkronizált, kollektív kaotikus viselkedését szabályozni [5].
Négy nikkelelektródból készített elektródrendszer kénsavban lejátszódó anódos oldódását úgy vizsgáltuk, hogy egyidejűleg mértük az elektródok egyedi és az elektródrendszer teljes áramát. Megállapítottuk, hogy a teljes áram (itot)kaotikus oszcillációja esetén az elektródok egyedi áramai (ik)szintén kaotikusan oszcillálnak, de eltérő fázisban. Az elektródrendszer kaotikus oszcillációját kétlépéses algoritmussal szabályoztuk. Először az elektródok kaotikus áramoszcillációját szinkronizáltuk4 úgy, hogy a velük sorba kapcsolt egyedi ellenállások értékeit (rk) folytonosan változtattuk a következő összefüggés szerint:
![]() ,
(12)
,
(12)
ahol k próbálgatással meghatározott csatolási állandó. Az 5. ábrán jól megfigyelhető a fázisszinkronizáció (S szakasz) hatása: a teljes áram itot amplitúdója számottevően megnövekedett. A szinkronizáltan, de még mindig kaotikusan oszcilláló elektródrendszert a Pyragas-módszerrel szabályoztuk (C szakasz); a bemutatott esetben például P_2 típusú oszcillációt stabilizáltunk. A szabályozás és a szinkronizáció megszüntetése után az elektródok egymástól függetlenül, kaotikusan oszcilláltak [5]. Ezek a kísérletek igazolták, hogy csatolt kaotikus rendszerek is szabályozhatók, ha valamilyen módon szinkronizálni tudjuk az alrendszerek kaotikus viselkedését.
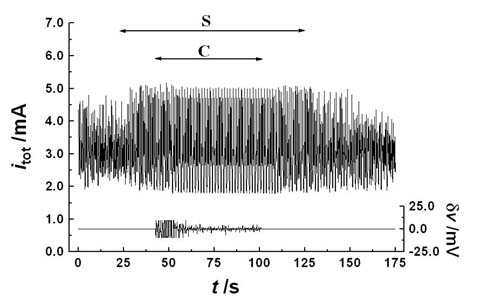
5. ábra. A teljes áram itot(mA) oszcillációja négy csatolt nikkelelektród kénsavban lejátszódó anódos oldódása során: S szakasz - fázisszinkronizáció; C szakasz - a szinkronizált kaotikus viselkedés szabályozása (P_2 oszcilláció stabilizálása) Pyragas-módszerrel [5]
A forgó rézkorong-elektród-nátrium-acetát/ecetsav elektrokémiai rendszerrel végzett kísérleteinkkel azt is igazoltuk, hogy a Pyragas-módszerrel nemcsak instabil periodikus pálya, hanem instabil egyensúlyi pont is stabilizálható (6. ábra). A látszólagos elektródpotenciált a (11) egyenlet szerint folytonosan perturbálva az oszcillálós áram helyett konstans áramot tudunk előállítani. Az egyenletben szereplő állandókat próbálgatással határoztuk meg [6].
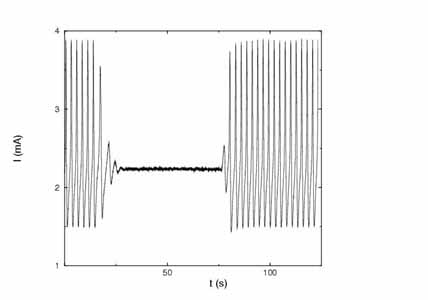
6. ábra. A Pyragas-módszer alkalmazása a forgó rézkorong-elektród-nátrium-acetát/ecetsav elektrokémiai rendszer instabil egyensúlyi pontjának stabilizálására [6]
Egy újabban javasolt folytonos káoszszabályozási módszer az ún. rezonanciakontroll alkalmazásáról számoltunk be [7] közleményünkben. A módszer elnevezése abból adódik, hogy ebben az esetben a paraméterperturbáció nagyságát a következő képlettel számítjuk:
dp(t)=gsin(2pnt), (13)
ahol g a perturbáció amplitúdóját, v pedig a frekvenciáját jelöli, melynek értékét az x(t) jelsorozat Fourier-spektrumából lehet meghatározni.
Káosz és rend
Mindennapi életünk tele van kaotikus jelenségekkel. A repülőgép szárnyának rezgése hirtelen kaotikussá válik, s a végeredmény elkerülhetetlen tragédia. A rakétát toló lángsugár egyik pillanatról a másikra remegni kezd, a masina irányíthatatlanná válik, a fedélzeten elhelyezett műhold pedig nem kerül Föld körüli pályájára. A vért periodikusan pumpáló szív megbetegszik, a szívverés szabálytalanná válik, és ha nincs segítség a közelben, a legrosszabb is bekövetkezhet. A káosz sokszor nemkívánatos, rossz. Megelőzhető ugyan, de ha minden óvintézkedésünk ellenére kialakul, sokáig úgy tűnt, kiszolgáltatottjai vagyunk az előre nem jelezhető folyamatoknak. A káoszszabályozási módszerek sikeres kísérleti alkalmazása biztató jele annak, hogy talán mégsem teljesen reménytelen a helyzet: a káosz megszelídíthető!
A káosz sikeres szabályozása még egy nagyon fontos lehetőséget nyújthat számunkra. Ahogyan az egyszerű oszcillációhoz rendelhető stabil határciklus belsejében megtalálható az instabillá vált egyensúlyi pont, úgy a kaotikus attraktor belsejében is megtalálható a káoszhoz vezető bifurkációk során instabillá vált valamennyi periodikus pálya. A káoszszabályozáskor tehát lehetőségeink száma szinte végtelen; egy kiválasztott dinamikai állapot stabilizálása után a szabályozó paraméter kicsiny megváltoztatásával könnyen átkapcsolhatjuk a rendszert egy másik dinamikai állapotba stb., tetszés szerint. A bonyolultnak tűnő feladat megoldása egyszerű: ha eldöntöttük, hogy pontosan melyik dinamikai állapotot szeretnénk előhívni a kaotikus attraktorból, a rendszert - kicsiny perturbációk alkalmazásával - a kívánt állapotnak megfelelő instabil fixpont kicsiny közelségébe tereljük, majd pedig ott tartjuk. (Hmm, lehet, hogy agyunk is így működik, s nem is olyan nagy baj, ha a fejünkben káosz uralkodik?!) Csak azt kell tudni, hogy mit mikor és miért csinálunk, s akkor a káosz előbb-utóbb oszlani kezd. Mert örökös a vágy és a feladat:
"Sarolt:
István fiam, nincs más
választás,
Rendet kell tenni,
rendnek kell lenni végre.
Rendet kell tenni,
rendnek kell lenni nálunk."
Szörényi Levente-Bródy János:István, a király (rockopera)
Az írás az OTKA T038071 sz. pályázat támogatásával készült.
1 Az itt is gyakran alkalmazott szakkifejezéseket (pl. kaotikus attraktor, ergodicitás, fázistér, Ljapunov-exponens, perturbáció, steady-state stb.) részletesen tárgyalja Tél Tamás és Gruiz Márton: Mi a káosz? (és mi nem az?) című sorozatindító cikke [12]. Ezen alapfogalmak pontos matematikai definíciója a sorozat közelmúltban megjelent cikkének (Krámli András: A káosz matematikusszemmel) glosszáriumában olvasható [13]. 2 A hipersík dimenziója - értelemszerűen - mindig pontosan eggyel kisebb, mint a kaotikus attraktor dimenziója.
3 Egyszerű arányos visszacsatolás.
4 A szinkronizáció hatását mutató, kísérleti adatokból készített animáció megtekinthető a következő címen: http://www.unideb.hu/~gasparv/doktori/4sync.avi (~2,4 MB).
IRODALOM
[1] Dyson, F.:
Infinite in All Directions; Harper: N. Y., 1988
[2] Petrov,
V.; Gáspár, V.; Masere, J.; Showalter, K.: Controlling Chaos in the
Belousov-Zhabotinsky Reaction, Nature, 361. kötet, 240-243.
o. (1993)
[3] Kiss, I. Z.;
Gáspár, V.; Nyikos, L.; Parmananda, P.: Controlling Electrochemical
Chaos in the Copper- Phosphoric Acid System, J. Phys. Chem. A, 101.
kötet, 8668-8674. o. (1997)
[4] Kiss, I. Z.;
Gáspár, V.: Controlling Chaos with Artificial Neural Network:
Numerical Studies and Experiments, J. Phys. Chem. A, 104. kötet,
8033-8037. o. (2000)
[5] Kiss, I. Z.;
Gáspár, V.; Hudson, J. L.: Experiments on Synchronization and Control
of Chaos on Coupled Electrochemical Oscillators, J. Phys. Chem.
B, 104. kötet, 7554-7560. o. (2000)
[6]
Parmananda, P.; Madrigal, R.; Rivera, M.; Nyikos, L.; Kiss, I. Z.;
Gáspár, V.: Stabilization of Unstable Steady States and Periodic
Orbits in an Electrochemical System using Delayed-feedback Control,
Phys. Rev. E, 59. kötet, 5266-5271. o. (1999)
[7]
Parmananda, P.; Madrigal, R.; Rivera, M.; Kiss, I. Z.; Gáspár, V.:
Resonant Control of Electrochemical Oscillations, J. Phys. Chem. B,
104. kötet, 11748-11751. o. (2000)
[8] Hübler, A.;
Lüscher, E.: Resonant Stimulation and Control of Nonlinear
Oscillators, Naturwissenschaften, 76. kötet, 67-69. o.
(1989)
[9] Ott, E; Grebogi,
C.; Yorke, J.: Controlling Chaos, Phys. Rev. Lett. 64. kötet,
1196-1199. o. (1990)
[10] Boccaletti, S.;
Grebogi, C.; Lai, Y.-C.; Mancini, H.; Maza, D.: The Control Of Chaos:
Theory And Applications, Phys. Rep. 329. kötet, 103-197. o.
(2000)
[11] Peng, B.;
Petrov, V.; Showalter, K.: Controlling Chemical Chaos, J. Phys.
Chem. US, 95. kötet, 4957-4959 o. (1991)
[12] Tél T.; Gruiz
M.: Mi a káosz? (és mi nem az?), Természet Világa, 133.
évf., 7. szám, 2002. július
[13] Krámli A.: A
káosz matematikusszemmel, Természet Világa, 135. évf., 7. szám,
2004. július
[14] Takens, F.:
Detecting strange attractors in turbulence. In Dynamical systems and
turbulence; Szerk.: Rand, D. A.; Young, L.-S., Lecture notes in
mathematics, 989. kötet, 366. o.; Springer: Heidelberg
(1981)
[15] Gáspár
V.: Játsszunk káoszt! Természet Világa, 133. évfolyam,
7. szám, 2002. július
[16] Hübinger, B.;
Doerner, R. Martiensen, W.; Herdering, M.; Pitka, R.; Dessler, U.:
Controlling Chaos Experimentally in Systems Exhibiting Large Effective
Lyapunov Exponents, Phys. Rev. E., 50. kötet, 932-948. o.
(1994)
[17] Pyragas, K.;
Tamasevicius, A.: Experimental Control of Chaos by
Delayed-Self-Controlling Feedback, Phys. Lett. A., 180. kötet,
99.-102. o. (1993)
| Természet Világa, | 136.
évfolyam, 8. szám, 2005. augusztus |