Szerkezet-hatás összefüggések (QSAR) 1.

Ebben a fejezetben az ún. "klasszikus" szerkezet-hatás összefüggésekkel foglalkozunk, vagyis amikor nem álltak/állnak rendelkezésre a térszerkezetet kezelő modern molekulagrafikai módszerek. Ezek természetesen bizonyos megszorításokkal, egyszerűbb esetekben jelenleg is jól használhatók, tehát amikor lehetőleg csak egyféle dolog elemzésére használjuk (csak felszívódás, csak in vitro hatáserősség, stb.)

Hansch–analízis

A kvantitatív szerkezet-hatás összefüggések (QSAR) keresése a molekulák mérhető fizikai-kémiai paramétereire, állandóira, valamint a mérhető biológiai aktivitásra, biológiai válaszra támaszkodik. A biológiai lehetnek aránylag egyszerűen mérhetőek, például enzimaktivitások, kötődési állandók, de lehetnek komplex in vivo adatok is. A fizikai-kémiai tulajdonságok is igen sokfélék lehetnek.

A különféle kezdeti próbálkozások közül a legismertebb és legáltalánosabban használt a Hansch és Fujita által az 1960-as évek elején leírt és az 1970-80-as években igen népszerűvé vált ún. lineáris szabadenergia modell volt. A kiindulási gondolat szerint a hatás több tényező függvénye:

Ebben bennefoglaltatik a hatóanyag transzportja és eloszlása, és a receptorral való kölcsönhatása is. Analóg (!) szerkezetű és azonos mechanizmus szerint ható molekulák hatása így leírható és számítható a fenti tényezőkből, a molekulák elektronkus, sztérikus, stb. viselkedése pedig leírható illetve összerakható egy alapmolekulához kapcsolódó szubsztituensek állandóiból. Ennek során három fő paraméterrel kell számolni:

• A megoszlási állandókon alapuló szubsztituens hidrofóbitási állandó;
• Az elektronikus hatásokat leíró Hammett-féle szubsztituens állandó;
• A térbeli viszonyokat tükröző Taft állandó

A hidrofóbitás jellemzésére Fujita 1964-ben egy új szubsztituens állandót vezetett be:

ahol P_x az x szubsztituenst tartalmazó származék oktanol/víz megoszlási hányadosa, P_H a szubsztituálatlan származék megoszlási hányadosa. A π állandók meghatározásához meg kell mérni a vegyületek megoszlási hányadosát. Ennek a klasszikus kirázásos technikával történő meghatározása precíz és hosszadalmas munkát igényel. Manapság sokszor (fordított fázisú) HPLC-vel határozzák meg, a kapott r_F értékek ugyanis arányosak log P-vel, például:

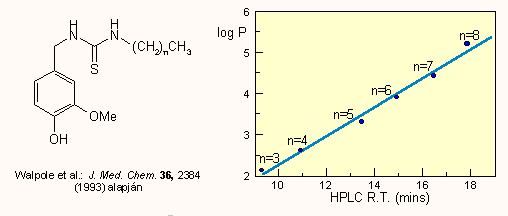
Ha szükség van a konkrét log P értékekekre, akkor természetesen az egyenest kalibrálni kell klasszikus úton is meghatározott adatokkal. Hansch és Leo szerint a megoszlási hányados fragmensekből is számolható:

A fragmensekből való kiszámolás nem 100%-osan megbízható, elsősorban az intramolekuláris kölcsönhatások miatt. A π értéke annál pozitívabb, minél inkább hidrofób (minél lipofilebb) egy szubsztituens.

A különböző szubsztituensek okozta elektronikus hatásokat leginkább a Hammett állandóval veszik figyelembe. A Hammett-féle σ állandó egy aromás szubsztituens hidrogénhez viszonyított elektronikus hatását tükrözi. A különbözőképpen szubsztituált benzoesavak K disszociációs állandója nagyban függ az o-, m- és p-szubsztituensektől, ezek elektronszívó és -taszító tulajdonságától, az induktív és mezomer effektusoktól. A σ_x = K_x / K_H állandót szubsztituens konstansnak nevezzük és általa sok egyéb folyamat sebessége, pl. benzoesav észterek k-val jellemezhető hidrolízise is kvantitatíve leírható az alábbi formában (Hammett egyenlet):

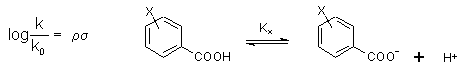
ahol ρ a reakcióra jellemző állandó. Nagysága a szubsztituensek befolyásának erősségére, előjele a reakció típusára (nukleofil, elektrofil) utal. A σ értéke elektronszívó szubsztituensek esetén pozitív és vice versa. A finomítások miatt a gyakorlatban többféle Hammett σ állandót alkalmaznak: a σ^p és σ^m a meta és para szubsztitensek esetére alkalmazzák, a σ⁺ értékeket az R-C₆H₄-CMe₂Cl származékok szolvolíziséből, a σ^- értékeket fenolok disszociációs állandójából vezették le. Orto helyzetű szubsztituensek esetén a Hammett összefüggés nem megbízható a térbeli gátlások miatt. Mivel az egyensúlyi ill. sebességi állandók logaritmusai arányosak a reakciót kisérő szabadenergia változással, ezért ezeket az összefüggéseket lineáris szabadenergia (pontosabban szabadentalpia) összefüggéseknek (LFER) szokták összefoglalólag hívni (bővebben lásd Szántay Csaba: Elméleti szerves kémia, vagy Peter Sykes: Mechanism in Organic Chemistry).

A Taft állandó a sztérikus hatások figyelembevételére született. A Taft egyenlet hasonló a fenti Hammett-egyenlethez, azonban itt az Taft állandó definíciója:

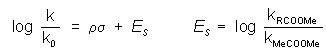
Az E_S a metilacetáthoz viszonyított savkatalizált hidrolízis állandókból származtatható.

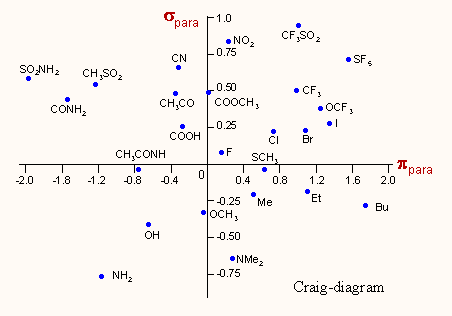
A szubsztituensek σ és π értékeit két dimenziósan ábrázolva az ún. Craig diagramot kapjuk ebből azonnal látható egy szubsztituens elektronszívó/küldő és hidrofil/hidrofób jellege, ami a tájékozódáson túlmenően jól felhasználható akár egy egyszerű "kézi tervezésnél" is. Az egészet faszerűen elágazó, döntési rendszerként alkalmazza a Topliss-féle kvalitatív tervezési módszer.

A fenti szubsztituens állandókat (amiket extratermodinamikai paramétereknek is szoktak hívni) Hansch kapcsolta össze a róla elnevezett egyenletté:

amely szerint a C ható koncentráció negatív logaritmusa arányos:

Ha az a együttható értéke nulla, akkor az összefüggés π-re nézve lineáris; természetesen a többi együttható is lehet nulla, ha egy-egy tagot nem veszünk figyelembe.

Néhány egyszerű irodalmi példával nézzük meg az elmondottak gyakorlatát.

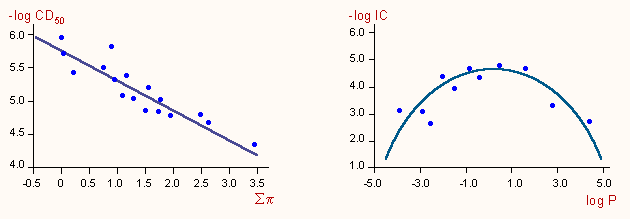
a) Az első egyszerű példa diklórfenil-amidinoizotiourea származékok antibakteriális hatását mutatja. Ezen regressziós egyenlet nélkül, egyszerű grafikus ábrázolással is tisztán látható, hogy a biológiai hatásnak a lipofilitás függvényében itt is optimuma van: maximális a hatás akkor, ha a két alkil szubsztituens "összege" 8-10 szénatom. Természetesen ha egyszerű alkil szubsztituensek helyett mindenféle egyéb csoportot vizsgálunk, ilyen egyszerűen, "szabad szemmel" nem lehet összefüggést találni.

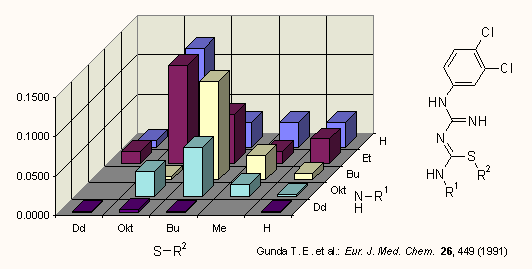
b) A következő példán egy baktériumból kapott alkohol dehidrogenáz enzim aktivitását elemzik R-CO-CH₃ típusú ketonokkal. Az enzim különböző sebességgel (k_rel) redukálja a metil-alkil ketonokat. Ismertek a kisérleti log k_rel adatok (függő változó), valamint log P és E_s (független változók).

                    log krel                              
    R:	        obsd.  calcd.  Δlog krel  log P     ES
-CH2CH3  	  1.08	 1.12	 0.04	   0.26	   -1.31
-CH(CH3)2	  0.48	 0.37	 0.11	   0.57	   -1.71
-ciklopropil     -0.10  -0.14	 0.04	   0.09	   -2.21
-CH2CH2CH3	  0.52	 0.42	 0.10	   0.79	   -1.60
-(CH2)3CH3  	  0.00	 0.11	 0.11	   1.32	   -1.63
-CH2CH(CH3)2	 -0.52	-0.63  	 0.11	   1.19	   -2.17
-CH(CH3)CH2CH3	 -1.00	-0.89	 0.11	   1.10	   -2.37
-(CH2)4CH3	 -0.05	-0.17	 0.12	   1.85	   -1.64
-(CH2)5CH3	 -0.22	-0.28	 0.06	   2.37	   -1.54
-(CH2)6CH3	 -0.52	-0.60	 0.08	   2.91	   -1.57
-(CH2)7CH3	 -1.00	-0.86	 0.14	   3.44	   -1.57
-(CH2)3Cl	  0.18	 0.39	 0.21	   0.50	   -1.72

A számítás során előszőr ezekből egy többváltozós lineáris egyenletrendszert kell alkotni:

1.08 = 0.26a - 1.31b + c
0.48 = 0.57a - 1.71b + c
… s.í.t.

Ezt a lineáris egyenletrendszert a legkisebb négyzetek módszerével közelítően megoldva megkapjuk az a, b és c regressziós együtthatókat. A példában két egyenletet is kiszámoltak, az egyikben csak log P, a másikban emellett E_s is szerepel. A második egyenlet segítségével számolt log k_rel értékek szerepelnek a táblázat második oszlopában, a harmadik oszlopban pedig a mért és számított érték közti eltérés látható.

A regressziós egyenletekhez meg szokás adni az adatok számát (itt n = 12), valamint különböző statisztikai jellemzőket: az ún. korrelációs együtthatót (vagy ennek négyzetét), ez egy 0 és 1 közötti szám és az összefüggés jóságát mutatja. Látható, hogy az első egyenlet esetében az összefüggés gyenge, a másodiknál igen jó (r = 0.982). Az s a szórás.

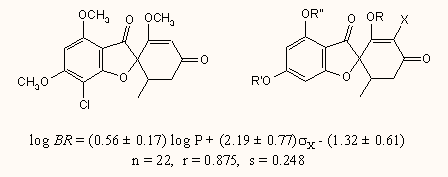
c) A harmadik példa egy orális gombaellenes antibiotikum, a grizeofulvin származékainak hatás–-szerkezet vizsgálatát mutatja be, az X szubsztituens függvényében. Mivel a regressziós egyenletben az X σ értékének nagy az együtthatója, ez arra utalhat, hogy az enon résznek jelentős szerepe lehet a bioaktivitásban.

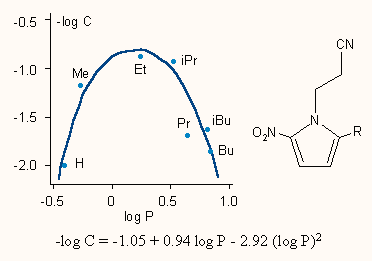
d) A negyedik példa néhány nitroimidazol származék gombaellenes hatását vizsgálja. Látható, hogy itt az összefüggés parabolikus, a hatásnak a lipofilitás függvényében maximuma van.

A fenti szubsztituens állandókon túlmenően még egy sor egyéb, az elektronikus vagy térbeli hatásokat tükröző fizikai-kémiai paraméterrel lehet találkozni az irodalomban:

• hidrofóbitás: kromatográfiás R_m, log s_w (vízoldékonyság). stb.
• sztérikus paraméterek: r_vdw, MV (moláris térfogat), sterimol értékek (ld. később)
• elektronikus hatások: pK, I_p, IR és NMR spektroszkópiai értékek, stb.
• kvantumkémiai adatok: E_HOMO, E_LUMO, q^π, q^σ, stb.

QSAR összefüggések felállításánál nagyon kell vigyázni arra, nehogy az összefüggés statisztikailag-matematikailag "túlhatározott" legyen, ekkor ugyanis bármilyen adatból szép, de értelmetlen összefüggést kaphatunk. Általában a vegyületek száma legalább 4-5-szöröse legyen a független változók számának. Másrészt a független változóknak egymástól is függetleneknek kell lennie (nem lehetnek kollinneárisak): hiba lehet például a molekula ugyanazon részében Hammet σ értékeket és kvantumkémiai úton számolt atomi töltéseket kombinálni egyazon regressziós egyenletben, mert mindkettő ugyanazt a dolgot fejezi ki. Ilyen problémák esetén használható a szokásos regressziós módszerek helyett az ún. PLS (partial least square) módszer, ezt azonban itt nem tárgyaljuk.

A Hansch egyenleten túlmenően mások is ismeretesek, röviden csak a Kubinyi féle bilineáris modellt említjük meg. A matematikai formulázás itt olyan, hogy P-nek itt is lehet maximuma, azonban parabolikus görbe helyett két metsző egyenessel végzi az illesztést: