![]() ,
(2.10)
,
(2.10)
káosz fn. 1.
Zűrzavar.
2.
Mit
Hitregékben: a világ keletkezését megelőző rendezetlen ősi állapot. [nk:lat<gör]
kaotikus mn
vál
Zűrzavaros.
A káosz szó használata arra a jelenségre, amit a tudományban kaotikusnak nevezünk valójában nem szerencsés. A szó köznapi értelme – „zűrzavar” – ugyanis számos félreértésre ad okot. Fokozottan igaz ez, ha felidézzük a szó eredeti görög jelentését is: „üresség”, „semmi”.
A káoszelmélettel foglalkozók, érzékelve a fogalom használata körüli zűrzavart, az angliai Royal Society szervezésében 1986-ban Londonban rendezett nemzetközi káoszkonferencián a következő definíciót javasolták a szótárkészítőknek:
chaos Math
Stochastic
behaviour occurring in a deterministic system.
káosz Mat
A
determinisztikus rendszerekben előforduló sztochasztikus viselkedés.
Ian Stewart az előszóban már idézett könyvében a következő frappáns mondatokkal kommentálja az angol nyelvű definíciót:
„That’s two more buzzwords – ‘stochastic’ and ‘deterministic’. Laplacian determinism is already familiar to us. ‘Stochastic’ means ‘random’. To understand the phenomenon of chaos we shall need to discuss their meanings further, because in its present form the definition is a paradox. Deterministic behaviour is ruled by exact and unbreakable law. Stochastic behaviour is the opposite: lawless and irregular, governed by chance. So chaos is ‘lawless behaviour governed entirely by law’.”
A káosz tehát olyan szabálytalan (véletlenszerű) viselkedés, amelyet teljes egészében szabályok (törvények) irányítanak. Zavaró paradoxon, valóban. A véletlenszerűség abban nyilvánul meg, hogy az ismert determinisztikus törvények ellenére sem tudjuk egy kaotikus rendszer viselkedését hosszútávon előrejelezni, mert a kaotikus mozgás önmagát sohasem ismétlő, aperiodikus mozgás.
Ilyen kiszámíthatatlan jelenségekkel szinte naponta találkozunk. Gondoljunk csak a gomolygó cigarettafüstre, a forró kávéban elkeveredő tejszínre, a hulló falevelek mozgására, a bazárokban kapható „örökmozgókra” vagy az időjárás változására. A hétköznapi ember, de a tudománnyal foglalkozó szakemberek többsége is azt mondaná, hogy az ilyen rendszerek viselkedése azért nem jósolható meg, mert nagyon bonyolultak, s olyan sok adatot kellene ismernünk a rendszer állapotának jellemzésére, hogy ezek hiánya lehetetlenné teszi egy jövőbeli állapot pontos kiszámítását. Ilyen alapon azonban már nem lehet megmagyarázni azt, hogy a csillagászok nem tudják megjósolni a Saturnus egyik – a bolygó körül egyébként szabályosan keringő, de pályája mentén „bukdácsoló” mozgást végző – krumpliforma holdacskájának, a Hyperionnak a pontos elhelyezkedését. Holott, az égi mechanika törvényei már évszázadok óta ismertek, és a feladat megoldása során csak néhány egyszerű testből álló mechanikai rendszer mozgását kellene előrejelezni. Hasonlóképpen nehezen értelmezhető, hogy például a BZ–reakció oszcillációs viselkedése bizonyos körülmények között kaotikussá is válhat, s így nem tudjuk előrejelezni az akár csak néhány perc múlva bekövetkező oszcilláció amplitudóját.
A káoszelmélet egyik legfontosabb felismerése az, hogy a determinisztikus rendszerek egyszerű törvényei is vezethetnek bonyolult viselkedésre. Az előrejelzés pontatlanságával kapcsolatban pedig azt kell figyelembe vennünk, hogy a kezdeti állapot leírására használt adatokat mindig csak véges pontossággal ismerjük.
E pontatlanság hatása elhanyagolható egy stabilis stacionárius (egyensúlyi) ponthoz vagy egy stabilis határciklushoz tartó rendszer esetében, s így a jövőbeli viselkedést könnyű megjósolni. Ezt a következőképpen érthetjük meg (Farkas, 1992). Az előrejelzés pontosságát a kezdetben egymáshoz nagyon közeli trajektóriák (a változók fázisterében megrajzolható pályavonalak) közötti távolság időbeli változásával jellemezhetjük. Tekintsük azokat a trajektóriákat, amelyek az n-dimenziós fázistér egy tetszőlegesen kiválasztott infinitezimális n-dimenziós gömbjének felületéről indulnak. Az idő előrehaladtával a fázistérben mozgó fázispontok által definiált felület elveszti szabályos gömbi alakját (hisz a mozgás nem minden irányban azonos sebességű), de mivel infinitezimális, egy n-dimenziós ellipszoid marad. Ha az ellipszoid ji(t) (i = 1, 2,…, n) főtengelyeinek értékében bekövetkező változás számítására egyszerű exponenciális függvényeket alkalmazunk:
![]() ,
(2.10)
,
(2.10)
és a trajektóriák mentén gyűjtött adatokból kiszámítjuk li, az ún. Ljapunov–kitevők értékét:
![]() (2.11)
(2.11)
úgy ezek összege a fázistér tágulásának mértékét fogja jellemezni.
Egy stabilis stacionárius pont minden irányban vonzó, így mindegyik Ljapunov–kitevője és ezek összege is negatív. A stabilis stacionárius pont körüli fázistér tehát nem kitágul, hanem összehúzódik. Aminek az a következménye, hogy a rendszer állapotának leírásában meglévő kezdeti pontatlanság annál kisebb hibát okoz egy jövőbeli állapot kiszámításában, minél távolabbi jövőre vonatkozik a jóslat.
A stabilis határciklus a zárt
görbe mentén történő perturbáció hatását nem csökkenti, azonban minden
más irányban vonzó
(l1=
0, li
< 0, ha i = 2, 3, …, n). Ahogyan egy bifurkáció során
a stacionárius pont elvesztheti stabilitását, úgy egy határciklus stabilitása
is megváltozhat. Egy T periódusidejű periodikus pálya bifurkációjakor
az instabilissá váló határciklus körül egy stabilis biperiodikus (2T
periódusidejű)
zárt trajektória jön létre, amelynek azonban már két neutrális iránya van
(l1=
0, l2=
0, li
< 0,
ha
i = 3, 4, …, n).
Mivel a Ljapunov–kitevők összege a határciklus és a biperiodikus attraktor
esetében is negatív, ezekre az objektumokra is igaz, hogy a nemneutrális
irányú kis perturbációk hatása időben csökkenni fog. A jövőbeli állapot
tehát nagy pontossággal megjósolható.
Gyakori, hogy a periódusketőződés
megismétlődik, és a biperiodikus oszcillációból, amit az egyszerűség kedvéért
jelöljünk P–2 típusúnak, P–4 típusú oszcilláció lesz. Ezt a bifurkációt
követheti még egy, majd még egy, majd még egy stb. Az egymást követő (n–1)-
és n-edik perióduskettőződéshez rendelhető bifurkációs paraméter
értékek különbsége, ![]() egyre kisebb lesz, s így a bifurkációs
diagramban lesz egy torlódási pont, ahol az attraktor periódusideje
végtelen naggyá válik. E torlódási ponton túl a káosz tartományába
érünk. A réz–ortofoszforsav elektrokémiai rendszer kísérleti bifurkációs
diagramját az alábbi ábra mutatja:
egyre kisebb lesz, s így a bifurkációs
diagramban lesz egy torlódási pont, ahol az attraktor periódusideje
végtelen naggyá válik. E torlódási ponton túl a káosz tartományába
érünk. A réz–ortofoszforsav elektrokémiai rendszer kísérleti bifurkációs
diagramját az alábbi ábra mutatja:
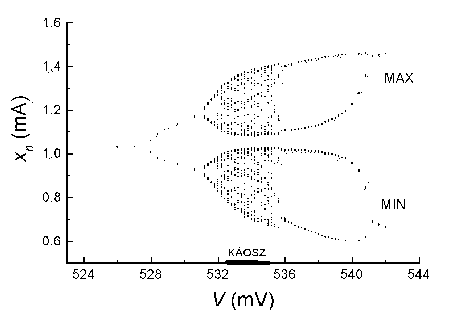 |
2.1. ábra A
réz–ortofoszforsav kaotikus elektrokémiai rendszer bifurkációs diagramja.
A bifurkációs paraméter a potenciosztáttal állandó értéken tartott „látszólagos" potenciál, a mért „jel" a teljes áram [6]. |
Feigenbaum (1979, 1980) elméleti megfontolások alapján megjósolta, hogy ezekben a perióduskettőződésekben Dpn értékei mértani sorozat szerint követik egymást:
![]() (2.13)
(2.13)
A káoszban uralkodó rend egyik legszebb példája, hogy a Feingenbaum–számnak elnevezett dállandó univerzális érvényű a perióduskettőződéssel képződő káoszra vonatkozóan, legyen szó fizikai, kémiai, biológiai, közgazdasági stb. rendszerről.
A bifurkációk sorozatával képződő végtelen periódusidejű határciklust kaotikus attraktornak nevezzük. A BZ–rendszer kaotikus attraktorát a [3]/1. ábra, az elektrokémiai rendszer kaotikus attraktorát pedig a [6]/5. ábra mutatja. A kaotikus attraktorra az jellemző, hogy létezik legalább egy pozitív Ljapunov–kitevője (l1> 0, l2= 0, li < 0, ha i = 3, 4, …, n). Mivel a fázistér a pozitív kitevőnek megfelelő irányban exponenciálisan tágul, a kezdetben egymáshoz közeli trajektóriák ugyan a kaotikus attraktoron maradnak, de időben szétválnak. A kezdeti feltételek megadásának infinitezimális hibája tehát exponenciálisan növekvő eltérést eredményez a számításokban, s így a jövőbeli állapot jóslása egyre pontatlanabbá válik. A kaotikus rendszerek ilyen értelmű érzékenységét a kezdeti feltételekre szokták tévesen – s ezzel sok félreértést okozva – „pillangó-effektusnak" nevezni.
Kaotikus állapot nem csak az itt ismertetett egyszerú perióduskettőződéssel, hanem többféle, ennél sokkal bonyolultabb mechanizmussal is kialakulhat. Ezek bemutatása azonban túlmutat az értekezés keretein. A témakörrel kapcsolatban az olvasó figyelmébe ajánlom Marek és Schreiber (1991) kitűnő tankönyvét.
A káosz tehát nem más mint állandósult instabilitás, amelyhez a fázistérben egy végtelen periódusú, azaz aperiodikus attraktor rendelhető. Az attraktor szó említése különösen fontos, mert jelzi, hogy a kaotikus állapotban sem lehetséges akármilyen mozgásforma, hisz a rendszer – elegendő idő elteltével – mindig a kaotikus attraktorra kerül. A determinisztikus káoszt pontosan ez különbözteti meg a valóban véletlenszerű zajtól.
A kémiában akkor beszélünk káoszról, ha egy kémiai jelenség aperiodikus.
Az oszcillációt eredményező egyszerű modellekből – elvben – igen könnyű kémiai káoszt mutató modelleket készíteni: például olyan új reakciókat kell egy oszcilláló modellhez hozzáadni, amelyek hatására perióduskettőződés következik be. Willamowski és Rössler (1980) közölte az első olyan, kémiai értelemben is reális modellt, amelyben a változók értékei mindig pozitívak és a reakciósebességi egyenletek kielégítik a kinetikai tömeghatástörvényt. Modelljük a Lotka–Volterra–modell bővítésének tekinthető:

A háromváltozós (X, Y és Z) séma azonban túlságosan bonyolult ahhoz, hogy ennek alapján kaotikus kémiai reakciót lehessen tervezni. Azt a következtetést azonban levonhatjuk, hogy a kémiai káosz kialakulásához legalább három köztitermék szükséges.
Hudson és Rössler (1984) később egy egyszerűbb modellt is kidolgozott:
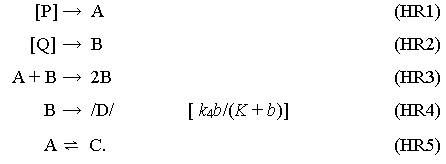
A HR–modellben felismerhetjük az Alternátorban szereplő autokatalízist és az autokatalitikus részecskét eltávolító elsőrendű reakciót. Ha C koncentrációját állandó értéken tarjuk, az egyszerű kétváltozós (A és B) modell csak Hopf–bifurkációt és határciklusos oszcillációt mutat. Ha azonban a C komponenst valódi köztiterméknek tekintjük, akkor a (HR5) reakció egyensúlyi jellege miatt C koncentrációváltozása visszahat az A és B köztitermékek oszcillációjára. Ez azonban még mindig nem elegendő a káoszhoz. Kaotikus oszcillációt csak akkor kapunk, ha a (HR4) reakció sebességét Michaelis–Menten típusú kinetikai egyenlettel írjuk le.
Egyszerű és a kinetikai tömeghatástörvényt minden szempontból kielégítő kaotikus reakciósémát elsőként Peng, Scott és Showalter (1990) javasolt:
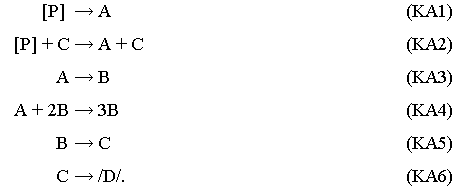
A kaotikus Autokatalátor-modell azáltal mutat káoszt, hogy az oszcillációt eredményező autokatalitikus ciklushoz egy olyan reakciót csatolunk, amelyben A képződését a C köztitermék katalizálja. E séma alapján még nem sikerült kaotikus kémiai reakciót tervezni, de egyszerűsége miatt fontos szerepe volt a káoszszabályozási eljárások kidolgozásában és egyszerűsítésében (Peng, 1991, 1992; Petrov, 1992).
A hidrogén-peroxid–szulfit–hidrogén-karbonát-rendszer CSTR-beli oszcillációját Rábai (1997) úgy tette kaotikussá, hogy a reakcióban képződő széndioxidot megfelelő sebességű nitrogén gázárammal eltávolította az oldatból. A káosz kialakulását a következő modellel értelmezte (Rábai, 1998):
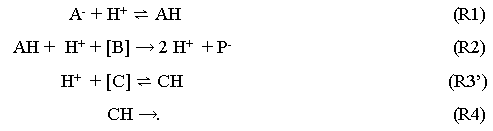
Az oszcillációs Rábai-modellből azáltal lett perióduskettőződést és káoszt mutató modell, hogy az eredetileg egyirányú (R3) reakciót Rábai megfordíthatóvá tette (R3’), s az új (R4) lépésben pedig gondoskodott a most már köztiterméknek számító CH eltávolításáról.
A BZ–rendszer CSTR-beli kaotikus viselkedéséről elsőként Schmitz, Graziani és Hudson (1979) számolt be. A BZ–reakció kaotikus oszcillációját az elmúlt két évtizedben számosan vizsgálták. A szerteágazó kísérletek eredményeiről részletes összefoglaló olvasható Scott (1993) korábban idézett könyvében. A kaotikus viselkedés értelmezése azonban – az Oregonátor-modell találomszerű „bővítgetésével” – sokáig nem járt sikerrel. A BZ–reakció legrészletesebb modelljének (Györgyi, 1990) szisztematikus redukciójával végül Györgyi és Field (1992) az alábbi négyváltozós reakciósémát vezette le:
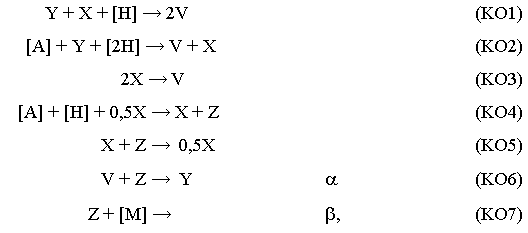
ahol [A] ş BrO3-, [H] ş H+, [M] ş CH2(COOH)2, X ş HBrO2, Y ş Br-, V ş BrCH(COOH)2 és Z ş Ce4+. A (KO6) és (KO7) folyamatok mellett feltüntetett a és b azt jelzi, hogy e két reakció sebességi együtthatóját (a redukció során alkalmazott egyszerűsítések következtében) változtatható paraméternek tekintjük. Az a és b változtatásának hatása hasonló ahhoz, amit az f sztöchiometriai állandó változtatása idéz elő az egyszerű oszcillációt mutató Oregonátor-modellben. A (KO1)–(KO7) reakcióséma kaotikus viselkedése abból ered, hogy a modellben két eltérő frekvenciájú periodikus folyamatot csatolunk: az egyik az Oregonátor-modell ismert oszcillációs ciklusa, a másik a brómmalonsav (V) ciklikus koncentrációváltozása. Ez utóbbi hatására a rendszer dinamikája egy oszcilláló és egy steady-state állapot között váltakozik. A brómmalonsav koncentrációja tehát a kaotikus BZ–rendszer „belső” bifurkációs paramétere.
Györgyi és Field – steady-state közelítést alkalmazva az Y változóra – a kaotikus Oregonátor-modell differenciálegyenlet-rendszerét egyszerűsítette, s így egy háromváltozós (x, v és z) dimenziómentes differenciálegyenlet-rendszert állított elő. Ezt használtuk mi is előszámításainkban, amelyek alapján megterveztük a BZ–rendszer kaotikus viselkedésének szabályozásakor alkalmazandó legígéretesebb kísérleti „stratégiát” [3].
Káoszszabályozási kísérleteink nagyobb részét elektrokémai rendszerekkel végeztük [6, 9, 11, 12]. A bemutatott egyszerű reakciósémák azonban nem alkalmazhatók a heterogén elektrokémiai folyamatokban megjelenő oszcilláció és káosz eredetének értelmezésére. Például, a rézelektród tömény ortofoszforsavban történő – általunk is vizsgált – anódos oldódása során a következő reakciók játszódnak le (Vidal, 1995):
![]() (V1)
(V1)
![]() (V2)
(V2)
ahol „ads" az elektród felületén adszorbeált, „aq" pedig a kevés vizet is tartalmazó elektrolit belsejében lévő részecskét jelöl. Valószínű, hogy egyik reakció sem elemi folyamat, s az elektrokémiai oldódás sebességmeghatározó elemi lépése a vízmolekulák lassú diffúziója az oldat belsejéből az elektród felületéhez. Az egyszerű (V1) és (V2) reakciók alapján sem oszcilláció, sem káosz megjelenése nem várható. Ismert azonban, hogy egy forgó rézkorong-elektród ortofoszforsavban történő anódos oldódása potenciosztatikus körülmények között kaotikus áramoszcillációt is eredményezhet (Schell, 1989).
Ez a jelenség azonban nem egyedi, s nem csak az anódos fémoldódás során figyelhető meg. Számos – potenciosztatikus vagy galvanosztatikus körülmények között – oszcilláló vagy kaotikus elektrokémiai rendszer ismert. Ezekről részletes beszámoló olvasható Hudson és Tsotis (1994) összefoglaló cikkében, amelyben több mint 500 (!) hivatkozás szerepel. Az elektrokémiai oszcillátorok általános vizsgálatát és csoportosítását Koper (1996) végezte el. Egyik fontos felismerése volt, hogy oszcilláció kialakulása elsősorban olyan rendszerekben várható, amelyekben az impedancia valós része bizonyos frekvenciatartományban negatív is lehet. Ezzel a kérdéskörrel kapcsolatos az értekezésben nem tárgyalt [18] közleményünk.
A réz–ortofoszforsav rendszer esetében az oszcillációhoz illetve káoszhoz vezető „nemlinearitás” eredetét az elektrokémiai fémoldódás Koper–Gaspard–modelljéből levezetett differenciálegyenlet-rendszer vizsgálata alapján érthetjük meg (Koper, 1992):
![]() (2.14)
(2.14)
![]() (2.15)
(2.15)
![]() ,
(2.16)
,
(2.16)
ahol v a potenciosztát alkalmazásával állandó értéken tartott (az ohmos esés hozzájárulását is tartalmazó) dimenziómentes „látszólagos" elektródpotenciál, e pedig a határfelületi kettősrétegen keresztül ható dimenziómentes „tényleges” elektródpotenciál. Az oldat belsejéből a forgó korongelektród felületéhez történő anyagáramlás leírására két diffúziós réteget tételezünk fel: az elektroaktív részecske dimenziómentes koncentrációja a fém felületéhez közelebbi rétegben u, a távolabbi rétegben pedig w. A dimenziómentes r, d és m állandók értéke összetett módon függ a rendszert jellemző egyéb paraméterektől (lásd Koper, 1992).
Vizsgálatunk célja szempontjából az a legfontosabb feltételezés, hogy a heterogén elektronátlépési reakció dimenziómentes k(e) sebességi együtthatója komplex módon függ e értékétől
![]() ,
(2.17)
,
(2.17)
ahol k1 és k2 sebességi együttható jellegű állandók, q a felület elektroaktív részecske általi borítottsága, n az elektrokémiai folyamatban résztvevő elektronok száma, a az ún. átlépési tényező, eo pedig a dimenziómentes standard elektródpotenciál. A borítottság változását a „tényleges” elektródpotenciál függvényében egy egyszerű szigmoidfüggvény alkalmazásával modellezzük:
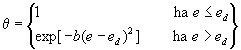 ,
(2.18)
,
(2.18)
amely azt fejezi ki, hogy a diffúzió-kontrollált tartományban (e Ł ed) a felület borítottsága teljes, a "tényleges" elektródpotenciál növelésével (e > ed) azonban a borítottság nullához tart.
A (2.17)–(2.18) egyenletek alapján számított polarizációs görbe – a kísérletekkel összhangban (pl. [6]/3. ábra) – bizonyos feszültségtartományban negatív meredekségű. Az egyenletek nemlineáris jellege azt is lehetővé teszi, hogy a rendszer instabilissá váljon és alkalmas körülmények között periodikus vagy kaotikus áramoszcilláció alakuljon ki. A (2.14)–(2.18) egyenleteket alkalmaztuk mi is azon előszámításainkban [6], amelyek alapján megterveztük a kaotikus áramoszcilláció szabályozásához szükséges kísérleti eljárást.