3.1.1 Kémiai káosz szabályozása
a BZ–reakcióban
A cériumion-katalizálta BZ–reakció
kaotikus viselkedését az SPF–módszer alkalmazásával szabályoztuk a következő
formula alapján:
ahol Dm
a szabályozó paraméter (a tápáramsebesség) kicsiny változtatását jelenti
az (n + 1)-edik ciklusban, An az n-edik
ciklusban mért amplitúdó (bromidion-szelektív elektród potenciálváltozás),
As
pedig
a stabilizálni kívánt, instabilis periodikus pálya amplitúdója. Ennek várható
értékét a kaotikus oszcilláció során mért
An+1–An
adatpárokból határoztuk meg az egydimenziós leképezés és a diagonális metszépontjaként.
A szabályozási állandót a nagy kísérleti zaj miatt ([3]/2.
ábra) nem tudtuk az SPF–módszer ismertetésekor leírt eljárással meghatározni,
így g
optimális értékét próbálgatással állapítottuk meg. A tápáramsebesség
(3.1) szerinti szakaszos perturbációjával P–1 és P–2 típusú oszcillációt
stabilizáltunk a kaotikus BZ–reakcióban [3].
 |
P-2 típusú oszcilláció szabályozása a kaotikus BZ-reakcióban. A kaotikus attraktor sárga, a szabályozott P-2 oszcillációnak megfelelő pálya piros. |
3.1.2 Káosz szabályozása elektrokémiai rendszerekben
3.1.2.1 Egyelektródos rendszerek
3.1.2.1.1 Káosz szabályozása
az OGY–elmélet alapján
A forgó rézkorong-elektród ortofoszforsavban
történő anódos oldódásakor potenciosztatikus körülmények között kialakuló
kaotikus áramoszcillációt a látszólagos elektródpotenciál szakaszos perturbációjával:
![]() ,
(3.2)
,
(3.2)
szabályoztuk. A (3.2) egyenletben
dV
a potenciálperturbáció, In a kaotikus áramoszcilláció
n-edik
ciklusában a kaotikus attraktor Poincaré–metszetén mért áram, Is
pedig
a stabilizálni kívánt periodikus pályát jellemző áram értéke a fixpontban.
E kísérletek jelentősége az, hogy ebben az esetben a szabályozási állandó
értékét meg tudtuk határozni. A (3.2) szerinti szakaszos pertubációkkal
P–1 (3.1. ábra) és P–2 típusú áramoszcillációkat stabilizáltunk [6].
 |
3.1. ábra
Kaotikus
áramoszcilláció szabályozása a réz–ortofoszforsav elektrokémiai rendszerben
(V = 532 mV, RW= 202 W, T = 255,65 K, w = 1800 rpm). A szabályozó algoritmust
35,2 s-nál kapcsoltuk be, és P–1 típusú oszcillációt stabilizáltunk;
Az alsó görbén jól látható, hogy a káosz- szabályozáshoz alkalmazott potenciál- perturbáció, dVn (mV), egyre csökkenő mértékű volt. Az algoritmust kikapcsolva (99,3 s) az áram ismét kaotikusan oszcillált [6]. |
 |
Szabályozott P-2 típusú oszcilláció a réz-ortofoszforsav
kaotikus elektrokémiai rendszerben.
A belső kis ábra a Poncaré-egyenesen (az attraktort metszú piros vonal) gyűjtött adatok alapján szerkesztett egydimenziós leképezést mutatja. |
3.1.2.1.2 Az átmeneti kaotikus
szakaszra vonatkozó hatványtörvény
Az OGY–elmélet szerint a szabályozó
algoritmus bekapcsolása és a szabályozás megtörténte közötti rövid, átmeneti
kaotikus szakasz időtartamának ![]() átlagértéke és a szabályozó paraméter változtatásának maximálisan megengedett
értéke (Dmmax)
között a következő összefüggés érvényes:
átlagértéke és a szabályozó paraméter változtatásának maximálisan megengedett
értéke (Dmmax)
között a következő összefüggés érvényes:
![]() ,
(3.3)
,
(3.3)
ahol g
ł1 a rendszer dinamikai tulajdonságaitól
függő állandó. A (3.3) egyenlet érvényességét a réz–ortofoszforsav elektrokémiai
rendszerrel végzett kísérletekkel igazoltuk (3.2. ábra) [6].
 |
3.2. ábra Az
OGY–elmélet
által megjósolt hatványtörvény kísérleti igazolása a réz– ortofoszforsav
kaotikus elektrokémiai rendszerrel végzett kísérletekkel; g
= 1,37 (+/- 0,05)
Dmmaxş dVmax [6]. |
3.1.2.1.3 Káoszszabályozás
mesterséges neuronhálózattal
Mesterséges neuronhálózati
algoritmusokat dolgoztunk ki a káoszszabályozás automatizálására, s az
eljárásokat sikerrel alkalmaztuk a réz–ortofoszforsav elektrokémiai rendszerre.
Kísérleteinkkel bizonyítottuk, hogy mesterséges neuronhálózatok „megtaníthatók"
egy kaotikus rendszer dinamikájára, s így szabályozási formulák alkalmazása
nélkül is „képesek" az instabilis periodikus pályák stabilizására (3.3.
ábra) [12].
 |
3.3. ábra (3–4–1) típusú mesterséges neuronhálózattal stabilizált P–1 típusú periodikus pálya (vastag vonal) a réz–ortofoszforsav elektrokémiai rendszer kaotikus attraktorában. Az attraktort az áramoszcilláció adatokból az ún. időeltolás módszerével (t = 0.5 s) állítottuk elő [12]. |
3.1.2.1.4 Káoszszabályozás
késleltetett visszacsatolással
Igazoltuk, hogy késleltetett visszacsatolással
(Pyragas-módszer) nem csak instabilis periodikus pálya, hanem instabilis
steady state is stabilizálható. A módszert a forgó rézkorong-elektród–nátrium-acetát/ecetsav
elektrokémiai rendszer kaotikus viselkedésének szabályozására alkalmaztuk
úgy, hogy a látszólagos elektródpotenciált folytonosan perturbáltuk a (3.4)
egyenlet szerint:
![]() ,
(3.4)
,
(3.4)
ahol dV(t)
a folytonosan alkalmazott potenciálperturbáció, i(t) és i(t
– t)
mért áramértékek, t
az ún. késleltetési idő, C pedig kísérletileg meghatározott állandó
[9].
3.1.2.2 Többelektródos rendszerek
Kísérleti módszert dolgoztunk ki
elektródrendszerek kaotikus viselkedésének szinkronizálására és szabályozására.
Nikkel-elektródokból készített elektródrendszer kénsavban történő anódos
oldódását úgy vizsgáltuk, hogy egyidejűleg mértük az elektródok egyedi
és az elektródrendszer teljes áramát. Megállapítottuk, hogy a teljes áram
(itot)kaotikus oszcillációja esetén az elektródok egyedi
áramai (ik)szintén kaotikusan, de nem azonos fázisban
oszcillálnak. Az elektródrendszer kaotikus oszcillációját kétlépéses algoritmussal
szabályoztuk. Először az elektródok kaotikus áramoszcillációját szinkronizáltuk
(3.4. ábra) úgy, hogy a velük sorbakapcsolt egyedi ellenállások értékeit
(rk) folytonosan változtattuk a következő összefüggés
szerint:
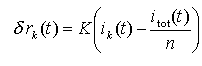 ,
(3.5)
,
(3.5)
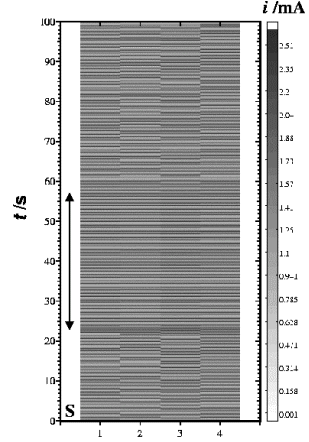 |
3. 4. ábra Kénsavban történő anódos oldódás során a négy nikkel-elektród egymástól független kaotikus áramoszcillációt mutat. Az (4.5) szerinti perturbációk hatására (K = – 80 W mA-1) az elektródok áramoszcillációja szinkronizálódik (S szakasz). A perturbációk megszüntetése után az elektródok ismételten egymástól függetlenül, kaotikusan oszcillálnak [11].
A mozi lejátszása után használja a Back gombot! |
3.2.1 Kémiai hullámok előállítása a BZ–rendszerben
3.2.1.1 Kémiai hullámok
gerjesztése lézerrel
Kimutattuk, hogy He–Ne lézer alkalmazásával
kémiai hullámok gerjeszthetők a batoferroin-katalizálta BZ–rendszerben.
Kísérleteink szerint a pontszerű megvilágítás hatására körhullámok vagy
kétcentrumú spirális hullámok képződnek a katalizátort tartalmazó poliszulfon
membrán felületén. A gerjesztési centrum(ok) kialakulását a megvilágított
membránfelületen lejátszódó lokális fotoredukciós folyamat BZ–rendszerre
kifejtett hatásával értelmeztük [10].
 |
a) redukált
állapot
b) besugárzás 5 s-ig /2 mm2 c) t = 6 s, erősebben redukált állapot a besugárzás helyén d) t = 16 s, az oxidáció kezdete e) t = 26 s, f) t = 40 s növekvő körhullámok |
3.2.1.2 Spirális hullámok
előállításának új módszere
Kísérleteinkben azt tapasztaltuk,
hogy a batoferroin-katalizálta BZ–rendszerben körhullámok helyett spirális
hullámok képződnek, ha elektrokémiai hullámgerjesztést alkalmazunk és a
gerjesztések periódusideje megközelíti az adott közegre jellemző ún. relaxációs
szakasz hosszát. Az összetett jelenség részletes magyarázatát nem ismerjük.
Feltételezzük, hogy szerepet játszik benne az ezüstelektród közelében képződő,
ezüst-bromidot tartalmazó „csapadékzóna”, az alkalmazott elektromos erőtér
és a gerjeszthető rendszerek jól ismert „sérülékenysége” is [5].
3.2.2 Kémiai hullámok csatolt BZ–rendszerekben
3.2.2.1 Jelátadás gerjeszthető
rendszerek között
Kísérleteink szerint a csatolt BZ–rendszerek
közötti „jelátadás" 1/n típusú rezonanciák formájában valósul meg.
Gerjeszthető BZ–elegyeket a kémiai hullámok számára átjárhatatlan vékony
fallal (plexi) választottunk el, amelybe egy rövid (~ 6,0 mm) kapilláris
csövecskét (d = 160 mm)
helyeztünk el. Így az egyik térfélben gerjesztett kémiai hullám (jel) –
áthaladva a kapillárison – kémiai hullámot (válaszjelet) gerjeszthet a
másik térfélben. Kísérleteinkben azt tapasztaltuk, hogy a körülményektől
függően mindegyik (n = 1) vagy csak minden n-edik (n
= 2, 3, 4, 5) „jel" tudott „válaszjelet" kiváltani. Részletesen vizsgáltuk
n
értékének változását a bromátion-koncentráció és a jelsorozat periódusidejének
függvényében. Modellszámításaink eredményei arra utalnak, hogy a gerjeszthető
rendszerek közötti jelátadás – elméletileg – az (n – 1)/n
(n ł3)
típusú rezonanciák formájában is megvalósulhat. A különböző rezonanciaformák
kialakulását és megjelenésük sorrendjét a periódusidő függvényében egy
egydimenziós leképezési eljárás segítségével értelmeztük [4].
3.2.2.2 Kémiai hullámok transzverzális
csatolása
Kísérletekkel és modellszámításokkal
is megmutattuk, hogy körhullámok transz-verzális csatolása spirális hullámokat,
spirális hullámok csatolása pedig bonyolult, térben és időben sokáig változó,
végül fázisszinkronizált mintázatokat eredményez. Kísérleteinkben ferroinnal
kezelt Nafion membránt alkalmaztunk, melynek egyik jellemző tulajdonsága
az, hogy BZ–hullámok csak a felületén terjedhetnek. A membrán két oldalán
kialakuló kémiai hullámok azonban a BZ–reakcióban kulcsszerepet játszó
semleges részecske, HBrO2, membránon keresztüli, spontán diffúziója
révén transzverzálisan csatolódhatnak (3.5. ábra). Modellszámításaink eredményei
arra utalnak, hogy már egyszerű síkhullámok csatolásakor is olyan komplex
hullámforrások alakulhatnak ki, amelyek véletlenszerű, külső perturbációk
hatására bonyolult mintázatokat hozhatnak létre [1,
2].
 |
3.5. ábra A ferroinnal kezelt és BZ–elegybe mártott Nafion membrán felületén képződött bonyolult mintázatok (4,5 óra). Különösen érdekes a kép baloldalán látható háromkarú spirál [1]. |
3.2.3 A BZ–hullámok diszperziós törvénye
3.2.3.1 A BZ–hullámok elméleti
diszperziós törvénye
A BZ–reakció Oregonátor-modelljéből
kiindulva levezettük a BZ–elegyben képződő kémiai hullámok diszperziós
törvényét:
![]()
![]() ,
(3.6)
,
(3.6)
ahol c(T) a T periódusidővel
képződő hullámok, cˇ pedig
egy magányos síkhullám állandósult terjedési sebessége. T*a
reakció mechanizmusából következő, s így a közeg összetételétől függő ún.
„kémiai időskála”. Az irodalomban közölt és saját mérésekből származó
kísérleti sebesség–periódusidő görbék elemzésével megmutattuk, hogy ![]() ahol Ts az adott közegben leggyorsabban forgó spirális
hullám periódusideje [7].
ahol Ts az adott közegben leggyorsabban forgó spirális
hullám periódusideje [7].
3.2.3.2 A ferroin-katalizálta
BZ–rendszerek empirikus diszperziós törvénye
A hullámfrontok spektrofotometriás
elemzése alapján javaslatot tettünk a ferroin-katalizálta BZ–rendszerek
empirikus diszperziós törvényére:
 ,
(3.7)
,
(3.7)
ahol Ctot a ferroin
teljes koncentrációja, t',
v*
és a
pedig a BZ–elegy összetételétől függő, a hullámprofil spektrofotometriás
elemzésével meghatározható kísérleti állandók. Azt találtuk, hogy a (3.6)
egyenlet levezetésekor alkalmazott egyik egyszerűsítő feltétel – lineáris
kapcsolat a hullám terjedési sebessége és a katalizátor oxidált formájának
koncentrációja között – csak egy szűk koncentrációtartományban érvényes
a ferroin-katalizálta BZ–rendszerekben. Ezt azzal értelmeztük, hogy a ferriin
redukciója nem írható le egyszerű pszeudo elsőrendű kinetikával [8].
3.2.3.3 Dimenziómentes diszperziós
törvény
A hullámdiffúziós-szám (M = p2/DT)
a diffúziós anyagtranszport kémai hullámok általi felerősítésének mértékét
jellemző dimenziómentes mennyiség. Értékét ![]() a T periódusidejű gerjesztések hatására képződő és egymástól
p
távolságra
haladó kémiai hullámok
belső
diffúziós együtthatójának (p2/T)
és a BZ–elegyre jellemző diffúziós együttható (D) értékének viszonyaként
számítjuk. A (3.6) egyenletből levezettünk egy dimenziómentes diszperziós
törvényt:
a T periódusidejű gerjesztések hatására képződő és egymástól
p
távolságra
haladó kémiai hullámok
belső
diffúziós együtthatójának (p2/T)
és a BZ–elegyre jellemző diffúziós együttható (D) értékének viszonyaként
számítjuk. A (3.6) egyenletből levezettünk egy dimenziómentes diszperziós
törvényt:
![]() ,
(3.8)
,
(3.8)
ahol x = T/Ts
dimenziómentes periódusidő, ![]() pedig az adott közegre jellemző dimenziómentes együttható. A (3.8) egyenlet
érvényességét az irodalomban közölt 13 független kísérletsorozat és saját
méréseink eredményeinek felhasználásával igazoltuk. Megállapítottuk, hogy
bár a ferroin-katalizálta rendszerek esetén a (3.7) szerint számított periódusidő
valóban jobb egyezést mutat a kísérleti értékekkel, a (3.8) szerinti skálázás
az ilyen rendszerekre is jól alkalmazható közelítés [7,
8].
pedig az adott közegre jellemző dimenziómentes együttható. A (3.8) egyenlet
érvényességét az irodalomban közölt 13 független kísérletsorozat és saját
méréseink eredményeinek felhasználásával igazoltuk. Megállapítottuk, hogy
bár a ferroin-katalizálta rendszerek esetén a (3.7) szerint számított periódusidő
valóban jobb egyezést mutat a kísérleti értékekkel, a (3.8) szerinti skálázás
az ilyen rendszerekre is jól alkalmazható közelítés [7,
8].
3.2.3.4 Univerzális diszperziós
törvény
A redukált hullámdiffúziós-szám,
m
= M(x)/M(1), fogalmának bevezetésével eljutottunk a BZ–hullámok
univerzális diszperziós törvényéhez:
![]() ,
(3.9)
,
(3.9)
Megmutattuk (4.6. ábra), hogy az
irodalomból ismert összes kísérleti adat – beleértve a ferroin-katalizálta
BZ–rendszerekben mérteket is – igen jó közelítéssel a (3.9) univerzális
diszperziós törvény alapján számítható elméleti görbére esik [7,
8].
 |
3. 6. ábra Az irodalomban közölt 13 független kísérletsorozat adataiból számított redukált hullámdiffúziós-szám, m, értékek ábrázolása a dimenziómentes periódusidő, x, függvényében. A folytonos vonal a (3.9) univerzális diszperziós törvény alapján számított elméleti görbe [7]. |