Some selected topics and publications

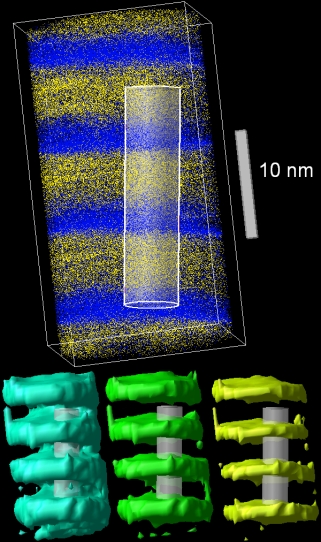Interface Sharpening in Miscible Alloys

We observed first by computer simulations that diffuse interfaces sharpen rather than broaden in completely miscible ideal binary systems. This was shown experimentally in situ during heat treatments at gradually increasing temperatures by scattering of synchrotron radiation in coherent Mo/V multilayers containing initially diffuse interfaces. To observe the sharpening by a ‘direct’ method which is able to show the atoms in the real 3D space, interfaces of Ni/Cu multilayers were studied by atom probe tomography. This effect provides a useful tool for the improvement of interfaces and offers a way to fabricate better x-ray or neutron mirrors, microelectronic devices, or multilayers with giant magnetic resistance.

Erdélyi Z, Sladecek M, Stadler Lorenz-M, Zizak I, Langer GA, Kis-Varga M, Beke DL, Sepiol B
Transient Interface Sharpening in Miscible Alloys
SCIENCE 306: pp. 1913-1915. (2004) Full text

Erdélyi Z, Szabó IA, Beke DL
Interface sharpening instead of broadening by diffusion in ideal binary alloys
PHYSICAL REVIEW LETTERS 89:(16) Paper 165901. 4 p. (2002) Full text

Balogh Z, Chellali MR, Greiwe GH, Schmitz G, Erdelyi Z
Interface sharpening in miscible Ni/Cu multilayers studied by atom probe tomography
APPLIED PHYSICS LETTERS 99:(18) Paper 181902. (2011) Full text

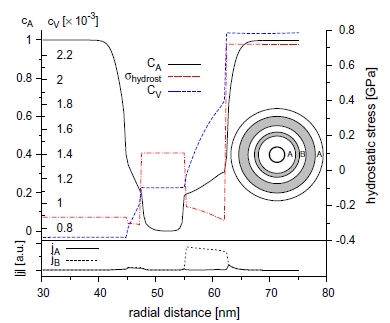Reactive diffusion and stresses in spherical geometry

We have developed a complete set of analytical equations to describe reactive diffusion in spherical core shell nanostructures. The model takes into account elastic stress, its plastic relaxation, as well as possible non-equilibrium vacancy densities. Furthermore, thermodynamic driving forces are included
to model formation of intermetallic product phases in intermediate composition range (NEW CONCEPT). We have applied the model to the reaction in spherical triple layers A/B/A and B/A/B, for which Schmitz et al. [Acta Mater 2009;57:2673] observed by atom probe tomography that growth rate depends on the stacking order. Comparison with experimental data have proved that significant deviations from vacancy equilibrium appear which control the stability and reaction rate of the nanometric diffusion couples.

Erdélyi Z, Schmitz G
Reactive diffusion and stresses in spherical geometry
ACTA MATERIALIA 60:(4) pp. 1807-1817. (2012) Full text

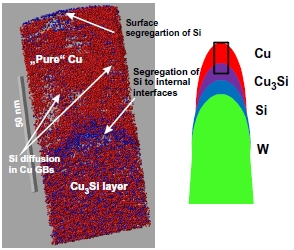Solid state reaction on the nanoscale

We have studied mainly Si based binary systems with high industrial potential, such as Ni-Si and Co-Si or Cu-Si. We have been interested in the formation of the product phases and their growth kinetics. To study the early stage of solid state reaction, besides theoretical ad computer simulation, we used a large variety of experimental techniques including synchrotron based techniques (XSW, GIXRF, EXAFS, XRD), secondary neutral mass spectrometry (SNMS), XPS, AES, TEM, atom probe tomography (APT).

Parditka Bence, Verezhak Mariana, Balogh Zoltán, Csik Attila, Langer Gábor A, Beke Dezs? L, Ibrahim Mohammed, Schmitz Guido, Erdélyi Zoltán
Phase growth in an amorphous Si–Cu system, as shown by a combination of SNMS, XPS, XRD and APT techniques
ACTA MATERIALIA 61:(19) pp. 7173-7179. (2013) Full text

Lakatos A, Langer GA, Csik A, Cserháti C, Kis-Varga M, Daróczi L, Katona GL, Erdélyi Z, Erdélyi G, Vad K, Beke DL
Nanoscale investigations of shift of individual interfaces in temperature induced processes of Ni-Si system by secondary neutral mass spectrometry
APPLIED PHYSICS LETTERS 97:(23) Paper 233103. 3 p. (2010) Full text

Erdélyi Z, Beke DL, Taranovskyy A
Dissolution and off-stoichiometric formation of compound layers in solid state reactions
APPLIED PHYSICS LETTERS 92:(13) p. Art.No. 133110. (2008) Full text

Anomalous diffusion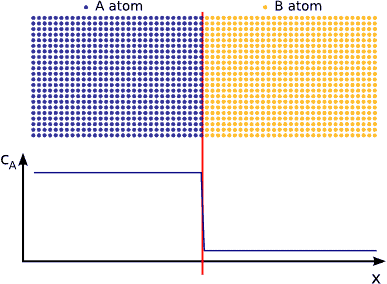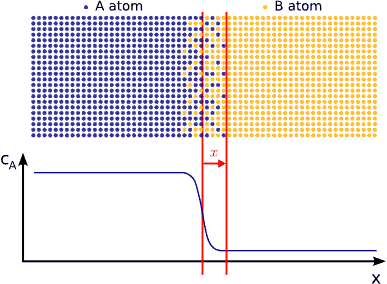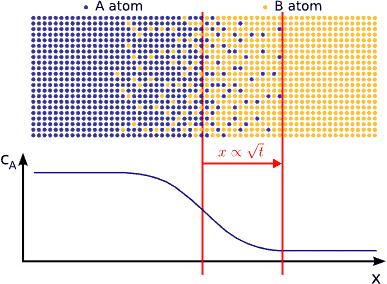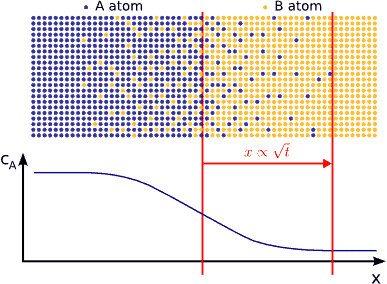

It is known from Fick’s phenomenological laws that, during annealing of a diffusion couple, the $$p$$ displacement of a plane with constant composition (or an abrupt interface) is proportional to $$t^{1/2}$$ or $$p^2 \propto t$$ (Fickian or normal shift kinetics with t equal to time). This is related to Einstein’s relation $$\langle R^2 \rangle \propto t$$, i.e., the mean square displacement of particles is proportional to the time, since Brownian motion of particles takes place in diffusion processes in ideal or dilute solids (even in other cases, a random walk or Brownian ’part’ is included in diffusion coefficients). Fick’s equations, however, do not allow modelling of a large number of diffusion phenomena. Departure from Brownian motion appears to be very common, so that anomalous diffusion would actually appear as normal. We have investigated diffusion on the nanoscale by both theoretically (including computer simulations) and experimentally and found numerous examples for anomalous kinetics.

Balogh Z, Erdélyi Z, Beke DL, Langer GA, Csik A, Boyen Hans-Gerd, Wiedwald U, Ziemann P, Portavoce A, Girardeaux Ch
Transition from anomalous kinetics toward Fickian diffusion for Si dissolution into amorphous Ge
APPLIED PHYSICS LETTERS 92:(14) p. Art.No. 143104. (2008) Full text

Katona GL, Erdélyi Z, Beke DL, Dietrich Ch, Weigl F, Boyen H-G, Koslowski B, Ziemann P
Experimental evidence for a nonparabolic interface shift on the nanoscale during the dissolution of Ni into bulk Au (111)
PHYSICAL REVIEW B 71: pp. 115421-1-5. (2005) Full text

Beke DL, Erdélyi Z
Resolution of the diffusional paradox predicting infinitely fast kinetics on the nanosale
PHYSICAL REVIEW B 73: pp. 035426-1-7. (2006) Full text

Erdélyi Z, Katona G, Beke DL
Nonparabolic nanoscale shift of phase boundaries in binary systems with restricted solubility
PHYSICAL REVIEW B 69: pp. 113407-1-4. (2004) Full text